Курсовая работа: Имитационное моделирование системы массового обслуживания

Присутствует такая операция, как помещение заявки на обслуживание в свободный канал. Просматриваются, начиная с первого, все каналы, когда выполняется условие timeOfFinishProcessingReq [ i ] <= 0 (канал свободен), в него подается заявка, т.е. генерируется время окончания обслуживания заявки.

for (int i = 0; i < channelCount; i++)

{

if (timeOfFinishProcessingReq [i] <= 0)

{

timeOfFinishProcessingReq [i] = GetServiceTime();

totalProcessingTime+= timeOfFinishProcessingReq [i];

break;

}

}

Обслуживаниезаявоквканалахмоделируетсякодом:

for (int i = 0; i < channelCount; i++)

{

if (timeOfFinishProcessingReq [i] > 0)

{

timeOfFinishProcessingReq [i] -= timeStep;

}

}

Алгоритм метода имитационного моделирования реализован на языке программирования C#.

3.3 Расчет показателей эффективности СМО на основе результатов ее имитационного моделирования

Наиболее важными являются такие показатели, как:

1) Вероятность отказа в обслуживании заявки, т.е. вероятность того, что заявка покидает систему не обслуженной.В нашем случае заявке отказывается в обслуживании, если все 2 канала заняты, и очередь максимально заполнена (т.е. 4 человек в очереди). Для нахождения вероятности отказа разделим время пребывания СМО в состоянии с очередью 4 на общее время работы системы.

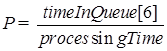
2) Относительная пропускная способность – это средняя доля поступивших заявок, обслуживаемых системой.

3) Абсолютная пропускная способность– это среднее число заявок, обслуживаемых в единицу времени.

4) Длина очереди, т.е. среднее число заявок в очереди. Длина очереди равна сумме произведений числа человек в очереди на вероятность соот