исправленная дисперсия, ,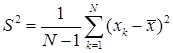

N – число прогонов программы, – надежность, .

2. Аналитическое моделирование СМО

2.1 Граф состояний системы и уравнения Колмогорова

Рассмотрим двухканальную систему массового обслуживания (n = 2) с ограниченной очередью равной шести (m = 4). В СМО поступает простейший поток заявок со средней интенсивностью λ = 4,8 и показательным законом распределения времени между поступлением заявок. Поток обслуживаемых в системе заявок является простейшим со средней интенсивностью μ = 2 и показательным законом распределения временем обслуживания.

Данная система имеет 7 состояний, обозначим их:

S₀ – система свободная, нет заявок;

S₁ – 1 заявка на обслуживании, очередь пуста;

S₂ – 2 заявки на обслуживании, очередь пуста;

S₃ – 2 заявки на обслуживании, 1 заявка в очереди;

S₄ – 2 заявки на обслуживании, 2 заявки в очереди;

S₅ – 2 заявки на обслуживании, 3 заявки в очереди;

S₆ – 2 заявки на обслуживании, 4 заявки в очереди;

Вероятности прихода системы в состояния S₀ , S₁ , S₂ , …, S₆ соответственно равны Р₀ , Р₁ , Р₂ , …, Р₆ .

Граф состояний системы массового обслуживания представляет собой схему гибели и размножения. Все состояния системы можно представить в виде цепочки, в которой каждое из состояний связано с предыдущим и последующим.

Рис. 3. Граф состояний двухканальной СМО

Для построенного графа запишем уравнения Колмогорова:

Чтобы решить данную систему зададим начальные условия:

Систему уравнений Колмогорова (систему дифференциальных уравнений) решим численным методом Эйлера с помощью программного пакета Maple 11 (см. Приложение 1).

Метод Эйлера

где- в нашем случае, это правые части уравнений Колмогорова, n=6.

(1)

Выберем шаг по времени . Предположим , где Т – это время, за которое система выходит на стационарный режим. Отсюда получаем число шагов . Последовательно N раз вычисляя по формуле (1) получим зависимости вероятностей состояний системы от времени, приведенной на рис. 4.

Значения вероятностей СМО при равны: