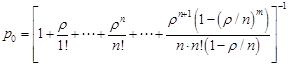Математика / Курсовая работа: Имитационное моделирование системы массового обслуживания

Курсовая работа: Имитационное моделирование системы массового обслуживания

– вероятность отказа (), т.е. вероятность того, что заявка покинет СМО не обслуженной;

– среднее число занятых каналов (k );

– среднее число заявок в СМО ();

– среднее время пребывания заявки в системе ();

– среднее число заявок в очереди () – длина очереди;

– среднее число заявок в системе ();

– среднее время пребывания заявки в очереди ();

– среднее время пребывания заявки в системе ()

– степень загрузки канала (), т.е. вероятность того, что канал занят;

– среднее число заявок, обслуживаемых в единицу времени;

– среднее время ожидания обслуживания;

– вероятность того, что число заявок в очереди превысит определенное значение и т.п.

Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания, среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (очереди), деленному на интенсивность потока заявок, т.е.

(1.4.1)

(1.4.2)

Формулы (1.4.1) и (1.4.2) называются формулами Литтла. Они вытекают из того, что в предельном стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих ее, т.е. оба потока заявок имеют одну и ту же интенсивность .