Курсовая работа: Інтеграли зі змінними границями
 ;
;
де х i - вузли, с i – ваги, R – залишковий член. Інтеграл приблизно заміняється сумою, схожою на інтегральну суму, причому вузли та коефіцієнти цієї суми не залежать від f ( x ) .
2. Квадратурні формули.
2.1. Формула прямокутників.
Припустимо, що f Î C 2 [- h /2, h /2] , h>0 .
 (2.1.1)
(2.1.1)
де f0 =f(0) , тобто площа криволінійної трапеції, обмеженої зверху графіком функції f(x) , апроксимується площею прямокутника, висота якого дорівнює значенню f(x) в середній точці трапеції (мал. 2.1.1).

мал. 2.1.1. Формула прямокутників
Знайдемо залишковий член , тобто похибку формули (2.1.1) . Нехай
![]() (2.1.2)
(2.1.2)
![]() Тому що F (0)=0 ,F / (0)= f 0 ,F // (0)= f / 0 ,F /// ( x )= f // 0 ,
Тому що F (0)=0 ,F / (0)= f 0 ,F // (0)= f / 0 ,F /// ( x )= f // 0 ,
то відповідно до формули Тейлора з залишковим членом у формі Лагранжа маємо
![]()
![]() (2.1.3)
(2.1.3)
деx- ,x+ - деякі точки , -h/x- <x+ <h/2.
Функція F ( x ) є первісної для f ( x ) . Тому для інтеграла, що стоїть в лівій частині наближеної рівності (2.1.1), з формули Ньютона-Лейбница з розрахунком (2.1.3) випливає наступне співвідношення

Ззвідси одержуємо формулу прямокутників із залишковим членом:
 (2.1.4)
(2.1.4)
2.2. Формула трапецій.
Нехай f Î C 2 [ 0 , h ] ,h>0
 (2.2.1)
(2.2.1)
де f 0 = f (0) , f 1 = f ( h ) тобто інтеграл  приблизно заміняється площею заштрихованої трапеції, показаної на малюнку (мал. 2.2.1).
приблизно заміняється площею заштрихованої трапеції, показаної на малюнку (мал. 2.2.1).

мал. 2.2.1. Формула трапецій.
Знайдемо залишковий член, тобто похибку формули (2.2.1). Виразимо f 1 та F 1 = F ( h ) де F - функція (2.1.2), по формулі Тейлора з залишковим членом в інтегральній формі (*) :
 (*)
(*)
![]() (2.2.2)
(2.2.2)
 (2.2.3)
(2.2.3)
Згідно (2.2.1) маємо
 (2.2.4)
(2.2.4)
Відокремивши в правій частині (2.2.3) доданок hf 0 /2 і замінивши його вираженням (2.2.4), з урахуванням того, що

знаходимо
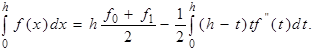
Перетворимо тепер другий доданок у правій частині, використовуючи узагальнену теорему про середнє. Тому що ( h - t ) t ³ 0 ,t Î [0, t ] то за теоремою
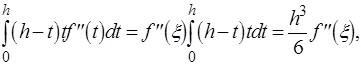
де x Î [ a , b ] - деяка точка . Підставляючи отримане в (*), приходимо до формули трапецій із залишковим членом :
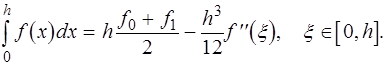 (2.2.5)
(2.2.5)
2.3. Формула Сімпсона .
Припустимо, що f Î C 4 [- h , h ] . Тоді інтеграл
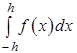
наближеного заміняємо площею заштрихованої криволінійної трапеції, обмеженою зверху параболою, що проходить через точки (- h , f -1 ) , (0, f 0 ) , ( h , f 1 ) , де fi = f ( ih ) (мал. 2.3.1)
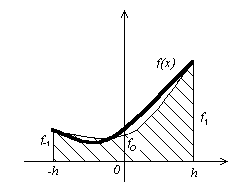
мал. 2.3.1 Формула парабол (Сімпсона)