Курсовая работа: Інтеграли зі змінними границями
у цьому неважко переконатися, поклавши x =- h ,x =0 ,x = h (її можна також одержати, побудувавши інтерполяційний багаточлен другого ступеня і приводячи подібні ). Звідси знаходь
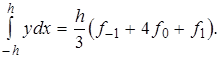
Таким чином, формула Сімпсона , називають також формулою парабол, має вид
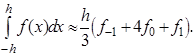 (2.3.1)
(2.3.1)
Покладемо F ± 1 = F ( ± h ) , де F функція (2.1.2). Оскільки F (0)=0, F ( k ) ( x )=
f ( k -1 ) ( x ), 1 £ k £ 5 то згідно формули Тейлора з залишковим членом в інтегральній формі маємо
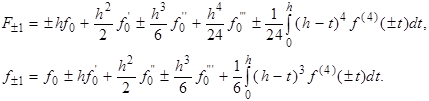
Звідси одержуємо
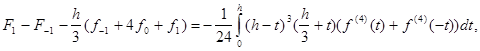 (2.3.2)
(2.3.2)
тому що інші члени взаємно знищуються.
Оскільки ![]() , t Î [0, h ] то застосовуючи до інтеграла (2.3.2) узагальнену теорему про середнє, знаходимо
, t Î [0, h ] то застосовуючи до інтеграла (2.3.2) узагальнену теорему про середнє, знаходимо
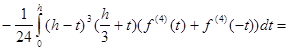
![]() (2.3.3)
(2.3.3)
де h Î [0, h ], x Î [- h , h ] - деякі точки. Приймаючи до уваги, що
![]()
з (2.3.2), (2.3.3) приходимо до формули
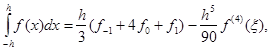 (2.3.4)
(2.3.4)
тобто до формули Сімпсона з залишковим членом.
3. Чисельні методи знаходження визначеного
Інтеграла зі змінною верхньою межею
У деяких випадках необхідно обчислити такі інтеграли
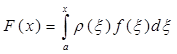
Можна, звичайно, розглядати його для кожного значення верхньої границі х як інтеграл зі сталими границями і обчислювати за однією з квадратурних формул, що невигідно у випадку великої кількості значень x. Краще вибрати деяку сітку і скласти таблицю значень інтеграла на цій сітці Fn = F ( x ) за квадратурної формули високої точності. Тоді
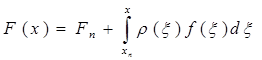
![]() (3.1)
(3.1)
причому останній інтеграл можна одчислювати за простими квадратурними формулами.
Окрім того, маючи таблицю F ( xn ) , можна знаходити F ( x ) інтерполяцією за цією таблицею. Природно, маючи і похідну інтегралаF ¢ ( x )= r ( x ) f ( x ) . Краще скористатись інтерполяційним поліномом Ерміта.
4.Опис обчислювального алгоритму
При реалізаціі алгоритму обчислення визначеного інтеграла зі змінними границями інтегрування використовуються процедури та функцiї, для того щоб скоротити витрати машинного часу при обчислюваннi, та для компактностi программи. Программа для знаходження написана на мовiDelphi5, стан пограмми – вiдлажена.
5. Обговорювання результатів
Таблиця 1
| Формула (3.1) | Формула Сімпсона | Формула трапецій | Дійсне значення інтеграла | |
| a=0; b=1; |
-0.7974398040 Різниця 0.0000012883 |
-0.7974386790 Різниця 0.0000001633 |
-0.7993252434 Різниця 0.00188672780 | -0.7974385156 |
| a=0; b=2; | 3.9190337956 Різниця 0.0000062805 | 3.9190353338 Різниця 0.0000047422 | 3.90875628130 Різниця 0.01028379486 | 3.9190400761 |
| a=0; b=3; | 10.5498688094 Різниця 0.00002744251 | 10.5498688094 Різниця 0.00002744251 | 10.5247085565 Різниця 0.02518769537 | 10.5498962519 |
| a=0; b=4; | 17.8842287345 Різниця 0.0000804723 | 17.8842201707 Різниця 0.00008903613 | 17.8382724576 Різниця 0.0460367491 | 17.8843092068 |
| a=0; b=5; | 25.5043003647 Різниця 0.0001835185 | 25.5042688642 Різниця 0.00021501907 | 25.4318420115 Різниця 0.0726418717 | 25.5044838833 |
| a=0; b=6; |
33.2576007639 Різниця 0.00035637138 | 33.2575244054 Різниця 0.00043272988 | 33.1529684530 Різниця 0.1049886822 | 33.2579571352 |