Курсовая работа: Інтегрування Нютона-Котеса
Задача чисельного інтегрування функції полягає в обчисленні значення визначеного інтегралу на основі ряду значень підінтегральної функції. Графічно інтеграл визначається площею‚ яка обмежена графіком функції 
.
Найчастіше на використовуються на практиці і є найбільш відомими наступні методи знаходження визначених інтегралів:
- методи Ньютона-Котеса‚ Гауса‚ Чебишева‚ що базуються на так званих квадратурних формулах‚ які одержуються шляхом заміни функції 
інтерполяційними многочленами;
- методи Монте-Карло‚ що базуються на використанні статистичних моделей.
1.2 Методи розв'язування задачі
Формули Ньютона-Котеса. Для виведення формул Ньютона-Котеса інтеграл (1) представляють у вигляді
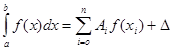‚ (2)
де 
- вузли інтерполяції‚ 
- коефіцієнти‚ залежні від виду формули‚ 
- погрішність квадратурної формули.
Здійснивши в (2) заміну підінтегральної функції відповідним інтерполяційним многочленом Лагранжа для 
рівновіддалених вузлів з кроком 
‚ можна отримати наступну формулу для розрахунку коефіцієнтів 
при довільній кількості вузлів
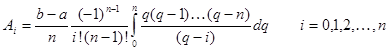(3)
де 
- приведена змінна.
Зазвичай‚ коефіцієнти 
називають коефіцієнтами Котеса. При цьому формула (3) набуває такого вигляду
. (4)
В таблиці 1 наводяться значення коефіцієнтів Котеса та оцінки погрішностей для значень від 1 до 8. Оскільки коефіцієнти Котеса при великій кількості ординат є доволі складними‚ то на практиці для наближеного обчислення визначених інтегралів розбивають проміжок інтегрування на велику кількість дрібних проміжків і до кожного з них застосовують квадратурну формулу Ньютона-Котеса з малим числом ординат. Таким чином‚ отримуються формули більш простої структури‚ точність яких може бути довільно високою.
Таблиця 1. Коефіцієнти Котеса.
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
1 |
1 |
1 |
К-во Просмотров: 871
Бесплатно скачать Курсовая работа: Інтегрування Нютона-Котеса
|
