Курсовая работа: Interpolation, approximation and differential equations solvers

· Linear interpolation

· Method of least squares interpolation

· Lagrange interpolating polynomial

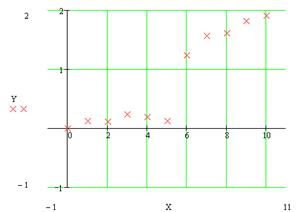
Fig 1. Initial data points

· Cubic spline interpolation

1.2.1 Linear interpolation

One of the simplest methods is linear interpolation (sometimes known as lerp). Generally, linear interpolation tales two data points, say and , and the interpolant is given by:

at the point

Linear interpolation is quick and easy, but it is not very precise/ Another disadvantage is that the interpolant is not differentiable at the point .

1.2.2 Method of least squares interpolation

The method of least squares is an alternative to interpolation for fitting a function to a set of points. Unlike interpolation, it does not require the fitted function to intersect each point. The method of least squares is probably best known for its use in statistical regression, but it is used in many contexts unrelated to statistics.

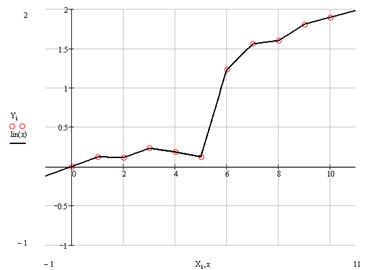
Fig 2. Plot of the data with linear interpolation superimposed

Generally, if we have data points, there is exactly one polynomial of degree at most going through all the data points. The interpolation error is proportional to the distance between the data points to the power n. Furthermore, the interpolant is a polynomial and thus infinitely differentiable. So, we see that polynomial interpolation solves all the problems of linear interpolation.

However, polynomial interpolation also has some disadvantages. Calculating the interpolating polynomial is computationaly expensive compared to linear interpolation. Furthermore, polynomial interpolation may not be so exact after all, especially at the end points. These disadvantages can be avoided by using spline interpolation.

Example of construction of polynomial by least square method

Data is given by the table:

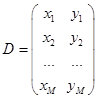
Polynomial is given by the model:

In order to find the optimal parameters the following substitution is being executed:

, , …,

Then: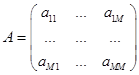

The error function:

It is necessary to find parameters , which provide minimums to function :