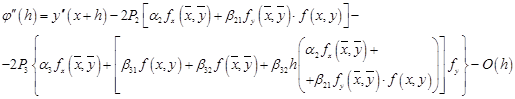
;

; ;

Thus we have system of equations:

Some of coefficients are already predefined:

; ; ; ; ; ; ;

Obtained results show that Runge-Kutta scheme for every order is unique.

Problem 4

4.1 Problem definition

Discuss the stability problem of solving the ordinary equation , via the Euler explicit scheme , say . If , how to apply your stability restriction?

4.2 Problem solution

The Euler method is 1st order accurate. Given scheme could be rewritten in form of:

If has a magnitude greater than one then will tend to grow with increasing and may eventually dominate over the required solution. Hence the Euler method is stable only if or:

For the case mentioned above inequality looks like:

Last result shows that integration step mast be less or equal to .

For the case , for the iteration method coefficient looks like

As step is positive value of the function must be less then . There are two ways to define the best value of step , the firs one is to define maximum value of function on the integration area, another way is to use different for each value , where . So integration step is strongly depends on value of .

References

1. J. C. Butcher, Numerical methods for ordinary differential equations, ISBN 0471967580