Курсовая работа: Interpolation, approximation and differential equations solvers

The following methods were described in this semester:

· Rectangular method

· Trapezoidal rule

· Simpson's rule

· Gauss-Legendre method

· Gauss-Chebyshev method

2.2.1 Rectangular method

The most straightforward way to approximate the area under a curve is to divide up the interval along the x-axis between and into a number of smaller intervals, each of the same length. For example, if we divide the interval into subintervals, then the width of each one will be given by:

The approximate area under the curve is then simply the sum of the areas of all the rectangles formed by our subintervals:

The summary approximation error for intervals with width is less than or equal to

Thus it is impossible to calculate maximum of the derivative function, we can estimate integration error like value:

2.2.2 Trapezoidal rule

Trapezoidal rule is a way to approximately calculate the definite integral. The trapezium rule works by approximating the region under the graph of the function by a trapezium and calculating its area. It follows that

To calculate this integral more accurately, one first splits the interval of integration into n smaller subintervals, and then applies the trapezium rule on each of them. One obtains the composite trapezium rule:

The summary approximation error for intervals with width is less than or equal to:

2.2.3 Simpson's rule

Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:

If the interval of integration is in some sense "small", then Simpson's rule will provide an adequate approximation to the exact integral. By small, what we really mean is that the function being integrated is relatively smooth over the interval . For such a function, a smooth quadratic interpolant like the one used in Simpson's rule will give good results.

However, it is often the case that the function we are trying to integrate is not smooth over the interval. Typically, this means that either the function is highly oscillatory, or it lacks derivatives at certain points. In these cases, Simpson's rule may give very poor results. One common way of handling this problem is by breaking up the interval into a number of small subintervals. Simpson's rule is then applied to each subinterval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the composite Simpson's rule.

Suppose that the interval is split up in subintervals, with n an even number. Then, the composite Simpson's rule is given by

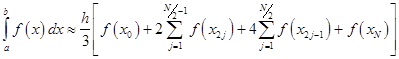
The error committed by the composite Simpson's rule is bounded (in absolute value) by

2.2.4 Gauss-Legendre method and Gauss-Chebyshev method

Since function values are given in fixed points then just two points Gauss-Legendre method can be applied. If is continuous on , then