The Gauss-Legendre rule G 2( f ) has degree of precision . If , then

,

where

It should be noted that even in case of two points method we have to calculate values of the function in related to , , this values could be evaluated by linear interpolation (because it is necessary to avoid oscillations), so estimation of integration error become very complicated process, but this error will be less or equal to trapezoidal rule.

Mechanism of Gauss-Chebyshev method is almost the same like described above, and integration error will be almost the same, so there is no reason to use such methods for the current problem.

Problem 3

3.1 Problem definition

It is well known that the third order Runge-Kutta method is of the following form

,

Suppose that you are asked to derived a new third order Runge-Kutta method in the following from

,

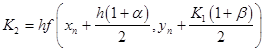
Find determine the unknowns , , and so that your scheme is a third order Runge-Kutta method.

3.2 Problem solution

Generally Runge-Kutta method looks like:

,

where coefficients could be calculated by the scheme:

The error function:

Coefficients , , must be found to satisfy conditions , consequently we can suppose that for each order of Runge-Kutta scheme those coefficients are determined uniquely, it means that there are no two different third order schemes with different coefficients. Now it is necessary to prove statement.

For , :

;

;

; ;
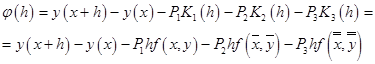