Курсовая работа: Интервальный анализ дохода трамвайного парка в очередные сутки с применением доверительной вероятности

Исходные данные – суточный доход трамвайного парка (млн. руб.):

12,56; 12,41; 12,52; 12,80; 12,98; 12,70.

Актуальные вопросы : Каков практический максимум суточного дохода трамвайного парка? В каких пределах практически будет находиться доход трамвайного парка в очередные сутки?

Сформулировать эти вопросы на языке теории вероятностей и дать на них ответы.

Высказать предположение (с обоснованием) о законе распределения суточного дохода трамвайного парка, найти оценки и построить доверительные интервалы для математического ожидания и дисперсии суточного дохода.

Решение

Исходный материал – данные наблюдений над суточным доходом трамвайного парка (млн. руб):

По условию известно:

х₁ =12,56; х₂ =12,41; х ₃ =12,52; х ₄ =12,80; х ₅ =12,98;х ₆ =12,70;n = 6.

Под X будем понимать случайную величину - доход, который получит трамвайный парк в будущий день. Данная величина дискретна, так как получить доход , например, 89,623 руб нельзя, существуют определенные стандарты. Но для решения этой задачи мы перейдем к идеализации и допустим, что π, е и др.– все это возможные значения X . Тогда X – непрерывная случайная величина.

Исчерпывающей характеристикой случайной величины является закон распределения, который зависит от условий проведения опыта. В нашем случае, опыт – это завтрашняя работа трамвайного парка. Учесть все условия невозможно. Может быть на следующий день резко возрастут цены на проезд в автобусах, и люди предпочтут пользоваться трамваями. А может это будет выходной, и людям просто захочется остаться дома. Так как же проанализировать условия?

1. В трамвайном парке работает множество трамваев. Пусть число трамваев – s .

2. Доход каждого трамвая завтра зависит от случая. Занумеруем трамваи:

1,	2,	3	…	h
,	,		…

3. Общий доход, который получат трамваи завтра:

X = +++…+

Т.е. X можно представить в виде суммы большого числа слагаемых. В силу центральной предельной теоремы мы можем ожидать, что закон распределения X близок к нормальному.

Пусть с – доход, который будет получен трамвайным парком в очередные сутки.

Событие является желательным событием. Найдем его вероятность.

Нам известно, что вероятность того, что X не превысит величины с , согласно нормальному закону распределения, зависит от с следующим образом:

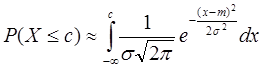
где m =M ( X ) – математическое ожидание X , =D (Х) – дисперсия, а - стандартное отклонение X . Эти константы можно оценить, используя формулы:

(млн.руб)

Следует отметить, что оценки и зависят от данных наблюдений, которые зависят от случая, когда m и от случая не зависят.

Зная оценки и , можно приближенно ответить на вопрос: «Какой доход (величина с ) получит трамвайный парк в очередной день, т.е. чтобы вероятность события была достаточно велика, например, равна ?» Величину с найдем из уравнения:

.

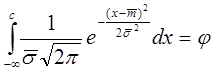Сделаем подстановку , тогда:

, ; при , ; при , .

Получим уравнение:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--