Выберем вероятность равной 0,95 (т.е. чтобы получить практический максимум суточного дохода трамвайного парка) и решим уравнение с помощью таблицы значений нормальной функции распределения. Получим:

; (млн.руб)

Таким образом, мы получили, что в очередные сутки практическим максимумом суточного дохода трамвайного парка будет являться 13,0132 млн. руб. Ответим на вопрос: «В каких пределах практически будет находиться доход трамвайного парка в очередные сутки?»

Общая формула:

, где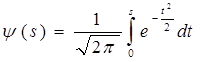

функция Лапласа, а a и b – концевые точки.

Пусть a и b расположены симметрично относительно m : a =m - s *; b =m + s *. Тогда:

,

т.к. функция нечетная. По таблицам найдем, что если s =1,96, то .

Таким образом, нам известно, что с вероятностью 0,95 Х будет находиться в пределах .

Т.е. доход трамвайного парка будет практически находиться в пределах от 12,262 до 13,077 млн. руб.

Как уже отмечалось, оценки и зависят от случая, в то время как m и от случая не зависят. О местоположении этих констант на числовой оси дают представление доверительные интервалы, т.е. такие интервалы, для которых до проведения наблюдений известна вероятность того, что они в итоге наблюдений накроют константу.

В нашем случае концевые точки доверительного интервала для m находятся по формулам: , , где

,

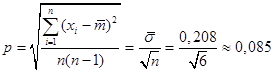а коэффициент зависит от устраивающей нас вероятности накрывания интервалом константы m :

.

можно найти из таблицы: при =0,95 и k =5(где k =(n -1) – число степеней свободы) =2,57.

Доверительный интервал для m : (12,45; 12,89) с вероятностью покрытия 0,95.

Концевые точки доверительного интервала для находятся по формулам:

, .

Вероятность того, что такой интервал накроет , обозначим:

Она зависит от чисел и . Выберем вероятность накрывания дисперсии, например, и воспользуемся таблицами для вычисления и . Для этого вычислим:

(1-α)/2=0,1 – погрешность слева; (1+α)/2=0,6 – погрешность справа, k =n -1=5 – число степеней свободы.

Значит =1,610; =9,24.

Интервал: (0,113; 0,646) – доверительный интервал для дисперсии с вероятностью покрытия 0,8.

Задание 2

Условие

В продолжение задания 1. Существенно ли изменились условия проведения опыта, если очередная серия наблюдений привела к следующим данным? Поставить этот вопрос на языке теории вероятностей и получить ответ.