Курсовая работа: Інженерна графіка
3 З точок поділу великого кола провести лінії, паралельні малій осі еліпса.
4 З точок поділу малого кола провести лінії, паралельні великій осі еліпса.
5 Визначити точки, які належать еліпсу: це точки, які обмежують велику та малу осі еліпса, та точки, знайдені у перетині допоміжних прямих (проведених відповідно до пунктів 3 та 4).
6 З’єднати точки, які належать еліпсу, за допомогою лекала. Для точності побудов поступово з’єднують по три точки.

Рисунок 1.13 – Поетапна побудова еліпса
Парабола – плоска крива, кожна точка якої рівновіддалена від директриси – прямої, перпендикулярної до осі симетрії параболи, та від фокуса – точки, яка належить осі симетрії параболи. Для побудови параболи існують кілька способів. На рисунку 1.14 наведена поетапна побудова параболи, яка здійснюється у такій послідовності:
1 За вихідними даними побудувати прямокутник CDEG.
1 Відстані DА та АEподілити на n рівних частин (у наведеному прикладі-6). З кожної точки ділення провести вертикальні лінії, паралельні осі параболи.
3 Сторони прямокутникаCD та EG ділять на таку саму кількість рівних частин (шість частин). Вершину параболи (точку А) з’єднують з вертикальними точками ділення.
4 У перетині допоміжних прямих одержують точки, які належать параболі.
5 Шукані точки поступово з’єднують за допомогою лекала.

Рисунок 1.14 – Поетапна побудова параболи
Синусоїда – плоска крива, утворена траєкторією точки кінця радіуса-вектора, який рівномірно обертається навколо центра і одночасно рівномірно поступально переміщується вздовж осі х. На рисунку 1.15 наведене поетапне виконання синусоїди. Вихідними даними є діаметр кола та період синусоїди.
Діаметр кола та відрізок періоду синусоїди поділити на будь-яку кількість рівних частин. Точки поділу кола позначені цифрами 1 – 11, а точки поділу відрізка періоду синусоїди – цифрами 11 – 111 . Точки синусоїди знаходять в перетині горизонтальних прямих, проведених з точок ділення кола, та вертикальних прямих, проведених через точки поділу відрізка періоду синусоїди. Шукані точки з’єднують плавною кривою за допомогою лекала.

Рисунок 1.15 – Поетапна побудова синусоїди
Спіраль Архімеда – плоска крива, утворена траєкторією точки, що рівномірно рухається вздовж радіуса-вектора, який, у свою чергу, рівномірно обертається навколо нерухомого центра.
Для побудови спіралі Архімеда (рисунок 1.16) за заданим її кроком (величина кроку дорівнює відрізку 0 11) необхідно з точки 0 провести коло, радіус якого дорівнює кроку. Поділити коло та крок на довільну кількість рівних частин: точки 11 -111 – це точки ділення кола, а точки 1 – 11 – точки ділення кроку.
Точки спіралі лежать на перетині радіальних променів, що сполучають точкиподілу кола та його центр, і дуг кіл, проведених через відповідні точки поділу кроку спіралі.
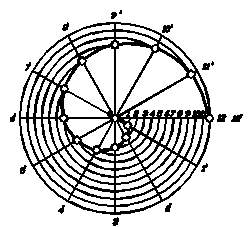
Рисунок 1.16 – Спіраль Архімеда
Евольвентою називають криву, що є траєкторією точки прямої лінії, що котиться без ковзання по нерухомому колу. На рисунку 1.17 наведений приклад побудови евольвенти. Щоб побудувати множину точок евольвенти, коло ділять на довільну кількість рівних частин (у наведеному прикладі-8). З кожної точки поділу проводять дотичну до кола, на якій відкладають відрізок, що дорівнює довжині дуги кола від початкової точки до заданої.
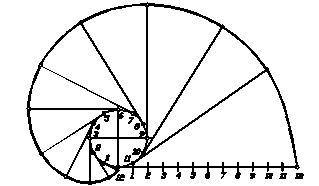
Рисунок 1.17 – Евольвента
Циклоїдами називають криві, які є траєкторією руху точки кола, що без ковзання котиться по прямій або кривій. Вихідними даними для побудови циклоїди є коло певного радіуса. На рисунку 1.18 наведений приклад побудови циклоїди.
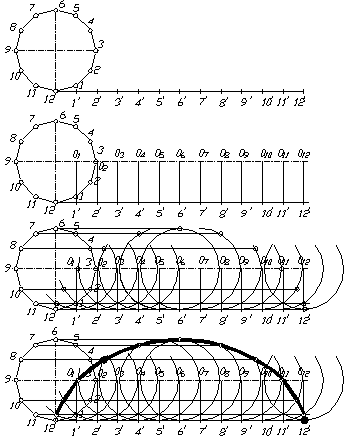
Рисунок 1.18 – Циклоїда