Курсовая работа: Использование информационных технологий в обучении геометрии

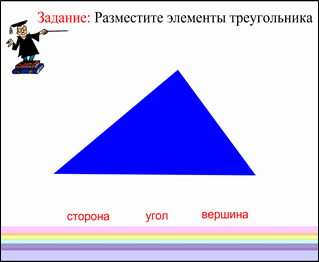
Учитель: Ваше первое задание: разместите элементы треугольника. Давайте вспомним названия всех элементов треугольника (сторона, вершина, угол – учитель убирает шторку, на словах задан эффект множественного клонирования).

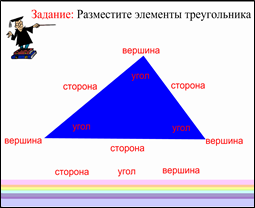
Учитель: Вот теперь их можно расставить (у доски работает 1 ученик).
Учитель: Молодцы ребята. Что общего у этих геометрических фигур на следующей странице?
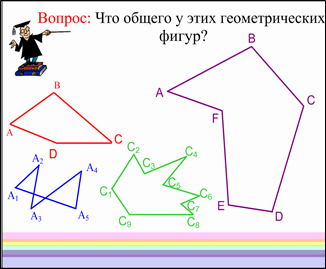
Учитель: Рассмотрим фигуру, составленную из отрезков AB, BC, CD, …, EF, FA так, что смежные отрезки (т. е. АВ и ВС, ВС и СD, …, EFи АВ) не лежат на одной прямой, а несмежные отрезки не имеют общих точек. Такая фигура называется многоугольником (рисунок на ИД). Точки А, В, С.....Е, Г называются вершинами, а отрезки АВ, ВС, ..., ЕF, FА — сторонами многоугольника. Сумма длин всех сторон называется периметром многоугольника.
Многоугольник с п вершинами называется п-угольником; он имеет п сторон. Примером многоугольника является треугольник. На рисунке изображены четырехугольник АВСDи шестиугольникАВСDEF. Фигура зелёного цвета, изображенная на этом рисунке не является многоугольником, так как несмежные отрезки А1 А5 и А2 А3 (а также А3 А4 и А1 А5 ) имеют общую точку.
Две вершины многоугольника, принадлежащие одной стороне, называются соседними. Отрезок, соединяющий любые две не соседние вершины, называется диагональю многоугольника.

Учитель: Следующее задание. Подпишите все элементы многоугольников. Нарисуйте диагонали (на слова диагональ и соседние вершины задан эффект множественного клонирования).
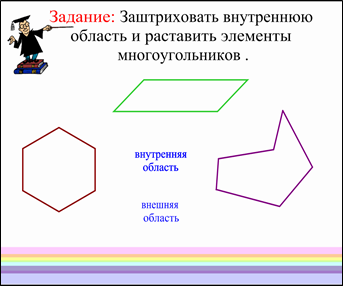
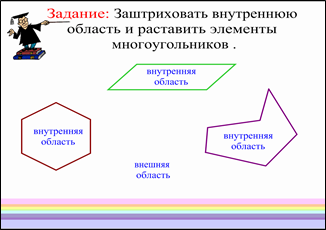
Учитель: Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника. На рисунке внутренние области многоугольников заштрихованы. Фигуру, состоящую из многоугольника и его внутренней области, также называют многоугольником. Наше новое задание: давайте заштрихуем все внутренние области многоугольников. А затем обозначим новые элементы многоугольника (Слова внизу экрана БЕЗ эффекта множественного клонирования, однако слова «внутренняя область» - это 3 наложенных друг на друга словосочетания, ровно для трёх областей, а слова «внешняя область» - только в одном экземпляре). После правильного расположения вид такой:
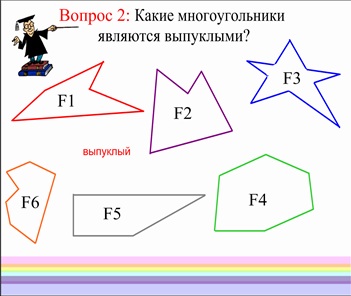
Учитель: Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Как вы думаете, ребята, правильно ли я расставила новые определения? Почему нет?
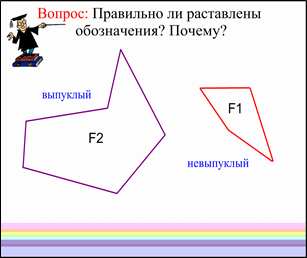
Учитель: Давайте проверим правильность вашего ответа опытным путем: проведём прямые линии через все соседние вершины обоих многоугольников (у доски 1 ученик маркером рисует прямые).
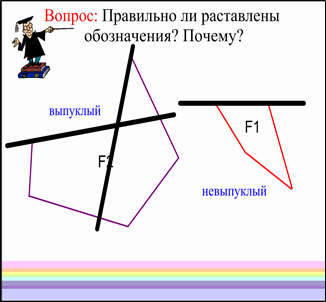
Учитель: Мы убедились, что на рисунке многоугольник F2 выпуклый, а многоугольник F1 невыпуклый.
1. Ответить на вопросы к рисунку на ИД (устно):
Вопрос 1. Какие фигуры, изображенные на доске, являются многоугольниками?
Учитель после обсуждения убирает или зачёркивает те рисунки, на которых изображены фигуры, не являющиеся многоугольниками.
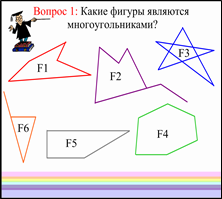
Вопрос 2. Какие многоугольники являются выпуклыми?
Учитель на ответы учеников расставляет подпись «выпуклый» (слово с эффектом множественного клонирования).