Курсовая работа: Использование модели экономического цикла Самуэльсона-Хикса

т.е. представляет собой систему неравенств

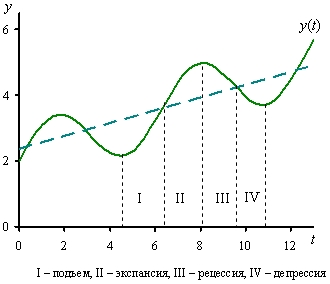
На рис. 4. устойчивому движению соответствуют области I (монотонное движение) и II (колебательное движение). Неустойчивому движению соответствуют области III (колебательное движение) и IV (монотонное). Области V соответствуют синусоидальные колебания с постоянной амплитудой.

[5]

Рис. 4. Стилизованные фазы экономического цикла

Разностные уравнения играют большую роль в экономической теории. Многие экономические законы доказывают с помощью именно этих уравнений, они используются в тех случаях, когда запаздывание оказывает существенное влияние на рассматриваемые процессы. В социально – экономических науках в целях простоты модели, связанные с запаздыванием, записывают в виде разностных уравнений, то есть в виде уравнений с дискретным временем. Наиболее широкое распространение разностные уравнения в экономической теории

Применение разностных уравнений в экономике представлено в моделях:

1. Модель рынка с запаздыванием сбыта.

2. Рыночная модель с запасами.

3. Динамическая модель Леонтьева.

4. Модель экономического цикла Самуэльсона – Хикса.

ГЛАВА 2. МОДЕЛЬ САМУЭЛЬСОНА-ХИКСА И ЕЕ ПРИМЕНЕНИЕ

2.1 Модель Самуэльсона-Хикса

Модель Самуэльсона-Хикса включает в себя только рынок благ, и поэтому уровень цен и ставка процента предполагаются неизменными; объем предложения благ совершенно эластичен.

Объем потребления домашних хозяйств в текущем периоде зависит от величины их дохода в предшествующем периоде

C_t = C_a,t + C_y y_{t -1} ,

где C_a - автономное потребление.

Предприниматели осуществляют автономные инвестиции, объем которых при заданной ставке процента фиксирован, и индуцированные инвестиции, зависящие от прироста совокупного спроса в предшествующем периоде

I_t = I_a,t + (y_{t -1} - y_{t -2} ).

На рынке благ установится динамическое равновесие, если

,(15)

гдеA_t = С _{a ,t} + I_{a ,t} .

Уравнение (15) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.

Уравнение (9.1) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.

При фиксированной величине автономных расходов (A_t = A = const) в экономике достигается динамическое равновесие, когда объем национального дохода стабилизируется на определенном уровне , т.е.y_t = y_{t -1} = y_{t -2} = ... = y_t-n = , где n - число периодов с неизменной величиной автономных расходов.

Из уравнения (15) следует, что = A /(1 - C_y ).

Посмотрим, какова будет динамика национального дохода, если в состоянии динамического равновесия изменится величина автономного спроса.

Освободимся от неоднородности в уравнении (15). Значения y_t и удовлетворяют равенству (15), поэтому можно записать следующее однородное конечно-разностное уравнение второй степени с постоянными коэффициентами:

,(16)