Курсовая работа: Использование модели экономического цикла Самуэльсона-Хикса
Так как yt = ![]() + yt , то направление изменения yt определяется направлением изменения
+ yt , то направление изменения yt определяется направлением изменения ![]() yt .
yt .
Из теории решения дифференциальных и конечно-разностных уравнений следует, что характер изменения ![]() yt зависит от значения дискриминанта характеристического уравнения. Поскольку в данном случае дискриминант равен (Cy +
yt зависит от значения дискриминанта характеристического уравнения. Поскольку в данном случае дискриминант равен (Cy + ![]() )2 - 4
)2 - 4![]() , то динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора и акселератора.
, то динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора и акселератора.
Если (Cy + ![]() )2 - 4
)2 - 4![]() > 0, то изменение yt происходит монотонно; при (Cy +
> 0, то изменение yt происходит монотонно; при (Cy + ![]() )2 - 4
)2 - 4![]() < 0 оно будет колебательным. Следовательно, график функции
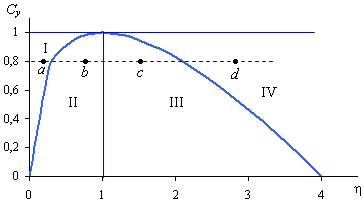
< 0 оно будет колебательным. Следовательно, график функции ![]() , изображенный на рис. 5, отделяет множество сочетаний Cy ,
, изображенный на рис. 5, отделяет множество сочетаний Cy , ![]() , обеспечивающих монотонное изменение yt , от множества комбинаций из значений Cy ,
, обеспечивающих монотонное изменение yt , от множества комбинаций из значений Cy , ![]() , приводящих к колебаниям yt .
, приводящих к колебаниям yt .
Устремляется ли значение yt к некоторой конечной величине или уходит в бесконечность, зависит от значения последнего слагаемого характеристического уравнения. Если ![]() < 1, то равновесие установится на определенном уровне. При
< 1, то равновесие установится на определенном уровне. При ![]() > 1 нарушенное 1 раз равновесие больше не восстановится. Когда
> 1 нарушенное 1 раз равновесие больше не восстановится. Когда ![]() = 1 , тогда значение yt будет колебаться с постоянной амплитудой.
= 1 , тогда значение yt будет колебаться с постоянной амплитудой.
 [6]
[6]
Рис. 5. Четыре областисочетаний Cy , ![]()
В результате все множество сочетаний Cy и ![]() оказалось разделенным на пять областей, как это показано на рис. 5. Если значения Cy и
оказалось разделенным на пять областей, как это показано на рис. 5. Если значения Cy и ![]() указывают на область I, то после нарушения равновесия в результате изменения автономного спроса значение yt монотонно устремится к новому равновесному уровню
указывают на область I, то после нарушения равновесия в результате изменения автономного спроса значение yt монотонно устремится к новому равновесному уровню ![]() При значениях Cy и
При значениях Cy и ![]() , находящихся в области II, национальный доход достигнет нового равновесного уровня, пройдя через затухающие колебания. Сочетания значений Cy и
, находящихся в области II, национальный доход достигнет нового равновесного уровня, пройдя через затухающие колебания. Сочетания значений Cy и ![]() , расположенные справа от перпендикуляра, опущенного из точки B на ось абсцисс, соответствуют нестабильному равновесию. Когда сочетания значений Cy ,
, расположенные справа от перпендикуляра, опущенного из точки B на ось абсцисс, соответствуют нестабильному равновесию. Когда сочетания значений Cy , ![]() указывают на область III, тогда динамика yt приобретает характер взрывных колебаний. Комбинации значений Cy ,
указывают на область III, тогда динамика yt приобретает характер взрывных колебаний. Комбинации значений Cy , ![]() в области IV приводят к тому, что после нарушения равновесия yt монотонно устремляется в бесконечность. И наконец, если акселератор равен единице, то при любом значении предельной склонности к потреблению в случае нарушения равновесия возникают равномерные незатухающие колебания yt .
в области IV приводят к тому, что после нарушения равновесия yt монотонно устремляется в бесконечность. И наконец, если акселератор равен единице, то при любом значении предельной склонности к потреблению в случае нарушения равновесия возникают равномерные незатухающие колебания yt .
2.2 Практическое применение модели Самуэльсона-Хикса
Пример
Заданы функция потребления домашних хозяйств: Ct = 50 + 0,8yt -1 и функция спроса предпринимателей на автономные и индуцированные инвестиции: It = 250 + ![]() (yt -1 - yt -2 ). В течение некоторого времени до периода t 0 включительно экономика находится в динамическом равновесии при спросе предпринимателей на автономные инвестиции в объеме 250 ден. ед. Это значит, что в каждом периоде производилось 1500 ед. благ, из которых 50 + 0,8·1500 = 1250 потребляют домашние хозяйства. С периода t 1 предприниматели решили, что объем автономных инвестиций должен равняться 350 ден. ед. Как в результате реализации этого решения будет меняться величина совокупного спроса (следовательно, и национального дохода) при четырех различных сочетаниях Cy ,
(yt -1 - yt -2 ). В течение некоторого времени до периода t 0 включительно экономика находится в динамическом равновесии при спросе предпринимателей на автономные инвестиции в объеме 250 ден. ед. Это значит, что в каждом периоде производилось 1500 ед. благ, из которых 50 + 0,8·1500 = 1250 потребляют домашние хозяйства. С периода t 1 предприниматели решили, что объем автономных инвестиций должен равняться 350 ден. ед. Как в результате реализации этого решения будет меняться величина совокупного спроса (следовательно, и национального дохода) при четырех различных сочетаниях Cy , ![]() , представленных на рис. 9.4 точками a (Cy = 0,8;
, представленных на рис. 9.4 точками a (Cy = 0,8; ![]() = 0,25), b (Cy = 0,8;
= 0,25), b (Cy = 0,8; ![]() = 0,75), c (Cy = 0,8;
= 0,75), c (Cy = 0,8; ![]() = 1,2) и d (Cy = 0,8;
= 1,2) и d (Cy = 0,8; ![]() = 2,3), показано в табл. 9.1-9.4.
= 2,3), показано в табл. 9.1-9.4.
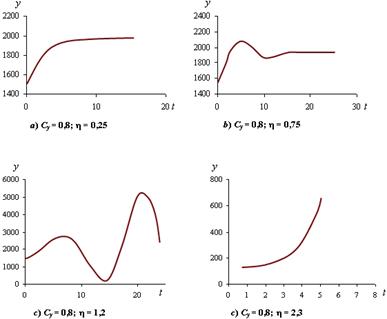
Рис. 6. Динамика национального дохода после изменения автономного спроса при различных сочетаниях Cy , ![]()
Таблица 2.1Динамика национального дохода при Cy = 0,8; ![]() = 0,25
= 0,25
| t | C | Ia | Iin | y |
| 0 | 1250 | 250 | 0 | 1500 |
| 1 | 1250 | 350 | 0 | 1600 |
| 2 | 1330 | 350 | 25 | 1705 |
| 3 | 1414 | 350 | 26,25 | 1790,3 |
| 4 | 1482,2 | 350 | 21,31 | 1853,5 |
| 5 | 1532,8 | 350 | 15,82 | 1898,6 |
| 6 | 1568,9 | 350 | 11,28 | 1930,2 |
| 7 | 1594,1 | 350 | 7,89 | 1952,0 |
| 8 | 1611,6 | 350 | 5,46 | 1967,1 |
| 9 | 1623,7 | 350 | 3,76 | 1977,4 |
| 10 | 1631,9 | 350 | 2,59 | 1984,5 |
| 11 | 1637,6 | 350 | 1,77 | 1989,4 |
| 12 | 1641,5 | 350 | 1,22 | 1992,7 |
| 13 | 1644,2 | 350 | 0,83 | 1995,0 |
| 14 | 1646,0 | 350 | 0,57 | 1996,6 |
| 15 | 1647,3 | 350 | 0,39 | 1997,7 |
| 16 | 1648,1 | 350 | 0,27 | 1998,4 |
| 17 | 1648,7 | 350 | 0,18 | 1998,9 |
| 18 | 1649,1 | 350 | 0,13 | 1999,2 |
| 19 | 1649,4 | 350 | 0,09 | 1999,5 |
| 20 | 1649,6 | 350 | 0,06 | 1999,6 |
| ... | ... | ... | ... | ... |
Таблица 2.2Динамика национального дохода при Cy = 0,8; ![]() = 0,75
= 0,75
| t | C | Ia | Iin | y |
| 0 | 1250 | 250 | 0 | 1500 |
| 1 | 1250 | 350 | 0 | 1600 |
| 2 | 1330 | 350 | 75 | 1755 |
| 3 | 1454 | 350 | 116,3 | 1920,3 |
| 4 | 1586,2 | 350 | 123,9 | 2060,1 |
| 5 | 1698,1 | 350 | 104,9 | 2153,0 |
| 6 | 1772,4 | 350 | 69,7 | 2192,1 |
| 7 | 1803,7 | 350 | 29,3 | 2183,0 |
| 8 | 1796,4 | 350 | -6,8 | 2139,5 |
| 9 | 1761,6 | 350 | -32,6 | 2079,0 |
| 10 | 1713,2 | 350 | -45,4 | 2017,9 |
| 11 | 1664,3 | 350 | -45,9 | 1968,4 |
| 12 | 1624,7 | 350 | -37,1 | 1937,6 |
| 13 | 1600,1 | 350 | -23,1 | 1927,0 |
| 14 | 1591,6 | 350 | -8,0 | 1933,7 |
| 15 | 1596,9 | 350 | 5,0 | 1951,9 |
| 16 | 1611,5 | 350 | 13,7 | 1975,2 |
| 17 | 1630,2 | 350 | 17,5 | 1997,6 |
| 18 | 1648,1 | 350 | 16,8 | 2014,9 |
| 19 | 1662,0 | 350 | 13,0 | 2024,9 |
| 20 | 1669,9 | 350 | 7,5 | 2027,4 |
| 21 | 1671,9 | 350 | 1,9 | 2023,8 |
| 22 | 1669,1 | 350 | -2,7 | 2016,3 |
| 23 | 1663,1 | 350 | -5,6 | 2007,5 |
| 24 | 1656,0 | 350 | -6,7 | 1999,3 |
| 25 | 1649,5 | 350 | -6,1 | 1993,4 |
| 26 | 1644,7 | 350 | -4,5 | 1990,2 |
| 27 | 1642,2 | 350 | -2,4 | 1989,8 |
| 28 | 1641,8 | 350 | -0,3 | 1991,5 |
| 29 | 1643,2 | 350 | 1,3 | 1994,5 |
| 30 | 1645,6 | 350 | 2,2 | 1997,9 |
| ... | ... | ... | ... | ... |
Таблица 2.3Динамика национального дохода при Cy = 0,8; ![]() = 1,2
= 1,2
| t | C | Ia | Iin | y |
| 0 | 1250 | 250 | 0 | 1500 |
| 1 | 1250 | 350 | 0 | 1600 |
| 2 | 1330 | 350 | 120 | 1800 |
| 3 | 1490 | 350 | 240 | 2080 |
| 4 | 1714 | 350 | 336 | 2400 |
| 5 | 1970 | 350 | 384 | 2704 |
| 6 | 2213,2 | 350 | 364,8 | 2928 |
| 7 | 2392,4 | 350 | 268,8 | 3011,2 |
| 8 | 2459,0 | 350 | 99,8 | 2908,8 |
| 9 | 2377,0 | 350 | -122,9 | 2604,2 |
| 10 | 2133,3 | 350 | -365,6 | 2117,8 |
| 11 | 1744,2 | 350 | -583,7 | 1510,5 |
| 12 | 1258,4 | 350 | -728,7 | 879,7 |
| 13 | 753,8 | 350 | -756,9 | 346,9 |
| 14 | 327,5 | 350 | -639,5 | 38,0 |
| 15 | 80,4 | 350 | -370,6 | 59,89 |
| 16 | 97,8 | 350 | 26,1 | 474,0 |
| 17 | 429,2 | 350 | 497,0 | 1276,2 |
| 18 | 1071,0 | 350 | 962,7 | 2383,6 |
| 19 | 1956,9 | 350 | 1328,9 | 3635,8 |
| 20 | 2958,7 | 350 | 1502,6 | 4811,3 |
| 21 | 3899,0 | 350 | 1410,5 | 5659,6 |
| 22 | 4577,7 | 350 | 1017,9 | 5945,6 |
| 23 | 4806,5 | 350 | 343,2 | 5499,7 |
| 24 | 4449,8 | 350 | -535,1 | 4264,7 |
| 25 | 3461,8 | 350 | -1482,0 | 2329,8 |
| ... | ... | ... | ... |
Таблица 2.4Динамика национального дохода при Cy = 0,8; ![]() = 2,3
= 2,3
| t | C | Ia | Iin | y |
| 0 | 1250 | 250 | 0 | 1500 |
| 1 | 1250 | 350 | 0 | 1600 |
| 2 | 1330 | 350 | 230 | 1910 |
| 3 | 1578 | 350 | 713 | 2641 |
| 4 | 2162,8 | 350 | 1681,3 | 4194,1 |
| 5 | 3405,3 | 350 | 3572,1 | 7327,4 |
| ... | ... | ... | ... | ... |
ЗАКЛЮЧЕНИЕ
Рассмотренная модель Самуэльсона-Хикса дает возможность сделать выводы о ?