Курсовая работа: Использование сетей Петри в математическом моделировании

(1; 0) | - (0;1).

Т-переход позволяет отразить в модели занятость некоторого устройства (подсистемы) в течение некоторого времени, определяемого параметром t (d). F-nepexod ("разветвление"). Графическое представление приведено на рис.4 в центре. Срабатывает при тех же условиях, что и Т-переход:

С содержательной точки зрения, F-переход отображает разветвление потока информации (транзактов) в системе.

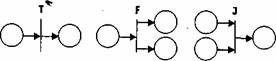
Рис.4. Графическое представление переходов Е-сети - Т-переход (слева), F-переход (в центре), J-переход (справа) J-переход ("объединение"). Графическое обозначение показано на рис.4 справа. Переход срабатывает при наличии меток в обеих входных позициях и отсутствии метки в выходной позиции: (1,1; 0) | - (0,0;1)

Он моделирует объединение потоков или наличие нескольких условий, определяющих некоторое событие.

Х-переход ("переключатель"). По сравнению с тремя предыдущими типами переходов, он содержит дополнительную управляющую ("разрешающую") позицию, которая графически обозначается обычно либо квадратиком, либо шестиугольником (рис.5, слева). Рис.5. Графическое представление переходов Е-сети, имеющих разрешающую позицию - Х-переход.

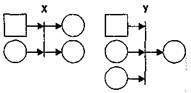
Рис.5. Графическое представление переходов Е-сети, имеющих разрешающую позицию - Х-переход (слева), Y-переход (справа)

Логика его срабатывания задается следующими соотношениями:

Х-переход изменяет направление потока информации (транзактов). В общем случае разрешающая процедура может быть сколь угодно сложной, но сущность ее работы заключается в проверке выполнения условий разветвления потока (с точки зрения программиста, разрешающая позиция аналогична условной инструкции типа if).

Y-переход ("выбор", "приоритетный выбор"). Этот переход также содержит разрешающую позицию (рис.5, справа). Логика срабатывания Y-перехода:

Y-переход отражает приоритетность одних потоков информации (транзактов) по сравнению с другими. При этом разрешающая процедура может быть определена различным образом: как операция сравнения фиксированных приоритетов меток; как функция от атрибутов меток (например, чем меньше время обслуживания, тем выше приоритет). В некотором смысле он работает аналогично инструкции выбора типа case. [12]

Еще раз подчеркнем, что в Е-сети все переходы обладают свойством безопасности. Это означает, что в выходных позициях (которые, в свою очередь, могут быть входными для следующего перехода) никогда не может быть более одной метки. Вместе с тем, в Е-сетях существуют понятия макроперехода имакропозиции, которые позволяют отображать в модели процессы накопления обслуживаемых транзактов в тех или иных узлах системы, а также расширить логические возможности Е-сетей.

Рассмотрим некоторые из них.

Макропозиция очередьпредставляет собой линейную композицию Т-переходов; суммарное количество выходных вершин-позиций определяет "емкость" очереди. Макропозиция генераторпозволяет представлять в сети источник меток (транзактов).

Если необходимо задать закон формирования меток, то "генератор" может быть дополнен разрешающей позицией.

Поскольку в Е-сети нельзя "накапливать" метки, то вводится макропозиция поглощения (или аккумулятор).

В целях повышения компактности и наглядности Е-сети для обозначения макропозиций используют специальные символы:

Q-очередь;

G - генератор;

А - аккумулятор.

Аналогичным образом, путем композиции N однотипных переходов могут быть получены макропереходы всех типов: XN, YN, JN.

Рассмотренные особенности Е-сетей существенно расширяют их возможности для моделирования дискретных систем вообще и параллельных процессов в частности. Ниже приведен пример описания в виде Е-сети мультипрограммной вычислительной системы (Рис.6). Обработка поступающих заданий организована в ней по принципу квантования времени: каждому заданию выделяется равный отрезок (квант) процессорного времени; если задание выполнено, то оно покидает систему, если же времени оказалось недостаточно, то задание встает в очередь и ждет повторного выделения кванта времени.

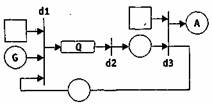
Рис.6. Пример описания вычислительной системы в виде Е-сети

На рисунке использованы следующие обозначения: