Курсовая работа: Использование сетей Петри в математическом моделировании

{

Spisok A;

Lref p,q; // Рабочие указатели.

Tref t;

int x,y; // Рабочие переменные.

// Фаза ввода.

cout << "Задайте отношение частичного порядка... \n";

cout << "Элемент ";

cin >> x;

cout << " предшествует элементу ";

while (x! =0)

{

cin >> y;

p = A. L (x); q = A. L (y);

t = new (Trailer); t->Id = q; t->Next = p->Trail;

p->Trail = t; q->Count += 1;

cout << "Элемент ";

cin >> x;

cout << " предшествует элементу ";

}

// Поиск ведущих с нулевым количеством предшественников.

A. Poisk ();

// Фаза вывода.

A. Vyvod ();

} [11]

§3. Математические модели с использованием сетей Петри

Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Их особенность заключается в возможности отображения параллелизма, асинхронности и иерархичности.

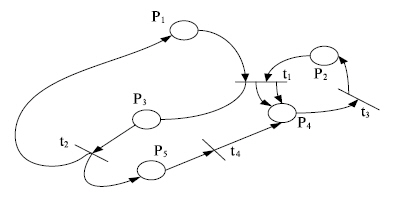
На рис.2 приводится пример сети Петри, где Р - конечное непустое множество позиций (состояний); Т - конечное непустое множество переходов (событий), причем p P и t_i T; F: Р x Т - {0, 1, 2,... }; Н: Т x Р {0, 1, 2,... } - функции входных и выходных инциденций; μ₀ : Р {0, 1, 2,... } - начальная маркировка. Вершины сети p P изображены кружками, а вершины t_i T - черточками (баркерами). Дуги соответствуют функциям инцидентности позиций и переходов. Точки в кружочках означают заданную начальную маркировку. Число маркеров в позиции равно значению функции μ: Р {0, 1, 2,... }. Переход от одной маркировки к другой осуществляется срабатыванием переходов. Переход t может сработать при маркировке μ, если он является возбужденным:

(1)