(1.4)

эквивалентна задаче поиска минимума функции

(1.5)

Часто условия задачи (1.1) - (1.3), содержащей ограничения только типа неравенств, бывает удобно записывать в сокращенной матричной форме

(1.6)

где с и x — векторы из пространства Rⁿ , b — вектор из пространства R^m , a А — матрица размерности m´ п.

Задачу линейного программирования, записанную в форме (1.1) - (1.3), называют общей задачей линейного программирования (ОЗЛП).

Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные x_j наложены условия неотрицательности, то она называется задачей линейного программирования в канонической форме, или канонической задачей линейного программирования (КЗЛП). В матричной форме КЗЛП можно записать в следующем виде:

(1.7)

Поскольку любая оптимизационная задача однозначно определяется целевой функцией f и областью D, на которой отыскивается оптимум (максимум), будем обозначать эту задачу парой (D, f).

Условимся относительно терминологии, которая используется в дальнейшем и является общепринятой в теории линейного программирования.

Планом ЗЛП называется всякий вектор х из пространства Rⁿ .

Допустимым планом называется такой план ЗЛП, который удовлетворяет ограничениям (1.2)-(1.3), т. е. содержится в области D. Сама область Dназывается при этом областью допустимых планов. Оптимальным планом х^* называется такой допустимый план, при котором целевая функция достигает оптимального (в нашем случае — максимального) значения, т. е. план, удовлетворяющий условию

maxf(x) = f(x^* ).

Величина f^* = f(x^* ) называется оптимальным значением целевой функции.

Решением задачи называется пара (х^* , f^* ), состоящая из оптимального плана и оптимального значения целевой функции, а процесс решения заключается в отыскании множества всех решений ЗЛП.

1.2 Переход к канонической форме

Подавляющее большинство известных методов решения задач линейного программирования предназначены для канонических задач. Поэтому начальный этап решения всякой общей задачи линейного программирования обычно связан с приведением ее к некоторой эквивалентной канонической задаче.

Общая идея перехода от ОЗЛП к КЗЛП достаточно проста:

-ограничения в виде неравенств преобразуются в уравнения за счет добавления фиктивных неотрицательных переменных , которые одновременно входят в целевую функцию с коэффициентом 0, т. е. не оказывают влияния на ее значение;

-переменные, на которые не наложено условие неотрицательности, представляются в виде разности двух новых неотрицательных переменных:

-переменные, на которые наложено условие неположительности, представляются в виде новой неотрицательной переменной помноженной на -1:

Нетрудно заметить, что «платой» за переход от общей формы задачи линейного программирования к канонической является рост ее размерности, что, при прочих равных условиях, является фактором, усложняющим процесс решения.

2. СИМПЛЕКС-МЕТОД

2.1 Теоретические основы симплекс-метода

Исходя из свойств линейных экстремальных задач, можно заключить, что на принципиальном уровне поиск их решений сводится к последовательному перебору угловых точек множества допустимых планов или, что то же самое, перебору соответствующих допустимых базисных планов. Средством решения данной проблемы явились прикладные оптимизационные методы, основанные на последовательном, целенаправленном переборе базисных планов ЗЛП.

Классическим методом решения ЗЛП стал симплекс-метод, получивший также в литературе название метода последовательного улучшения плана (упорядоченность обеспечивается монотонным изменением значения целевой функции при переходе к очередному плану), разработанный в 1947 г. американским математиком Джорджем Данцигом.

Пусть стоит задача максимизации

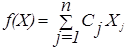(2.1)

при условиях