Курсовая работа: Использование среды MatLAB для решения линейной программы
Xj ³ 0, j=1,…,n(2.3)
Предположим, что нам удалось найти опорный план X0 , в котором, например, первые m компонент отличны от нуля:
X0 =(X1 0 ,X2 0 ,…,Xm 0 , 0, …, 0), (2.4)
и соответствующий базис Б=(A1 ,A2 ,…,Am ).
Попытаемся выбрать другую систему базисных векторов с целью построения нового опорного плана, в котором k-я переменная (k>m) принимает значениеQ >0:
X(Q) = (X1 (Q), X2 (Q),…,Xm (Q), 0, …,Q, … 0) (2.5)
Подставляя (2.4) в (2.2), имеем
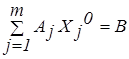(2.6)
Подставив (2.5) в (2.2), получаем
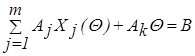(2.7)
Разложим вектор Ak по векторам исходного базиса
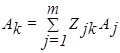(8)
В общем случае для получения коэффициентов такого разложения придется решать систему mуравнений с m неизвестными, которая имеет единственное решение, поскольку базисные векторы линейно независимы и соответствующая матрица имеет ненулевой определитель. Заметим, что в ситуации, когда базисные векторы являются единичными (образуют единичную матрицу), искомые коэффициенты совпадают с компонентами исходного вектора; поэтому в дальнейшем мы предпочтем работать с единичным базисом.
Подставляя (2.6) и (2.8) в (2.7), получаем
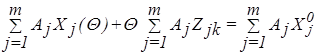, (2.9)
откуда имеем
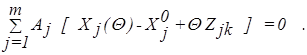(2.10)
Так как система уравнений (2.10) имеет единственное решение, то получаем представление первых mкомпонент нового плана
(2.11)
Естественно потребовать неотрицательность компонент нового плана. Так как нарушение неотрицательности в (2.11) может возникнуть лишь при Zjk >0, то значение Q нужно взять не превышающим наименьшего из отношений 
к положительным Zjk .
Если к тому же учесть, что число положительных (базисных) компонент опорного плана должно оставаться равным m, то одну из первых m (ненулевых) компонент исходного плана обращаем в нуль выбором
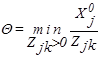(2.12)
Подставляя (2.11) в (2.1), имеем
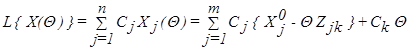(2.13)
Если обозначить
, (2.14)
, (2.15)
то (2.13) примет вид
(16)