Курсовая работа: Исследование прочности на разрыв полосок ситца

Гистограммой частот называется фигура, состоящая из прямоугольников с равными основаниями (длина интервала) и площадью численно равной частоте.

Для построения гистограммы воспользуемся таблицей:

xi <x≤xi+1	(27; 29]	(29; 31]	(31; 33]	(33; 35]	(35; 37]
ni	4	47	56	22	1
hi = ni Δx	4/2	47/2	56/2	22/2	½

	Δx=2
hi
56⁄ 2
47⁄ 2
22⁄ 2
4/2
1/2
27	29	31	33	35	37
xi

Гистограммой относительных частот называется фигура, состоящая из прямоугольников с равными основаниями (длина интервала) и площадью численно равной относительной частоте.

Для построения гистограммы воспользуемся таблицей:

xi <x≤xi+1	(27; 29]	(29; 31]	(31; 33]	(33; 35]	(35; 37]
Р* i	4/130	47/130	56/130	22/130	1/130
hi = P* i Δx	4/260	47/260	56/260	22/260	1/260

Δx=2

h*i
56∕ 260
47⁄ 260
22⁄ 260
4∕ 260
1 ∕ 260
0	27	29	31	33	35	37
xi

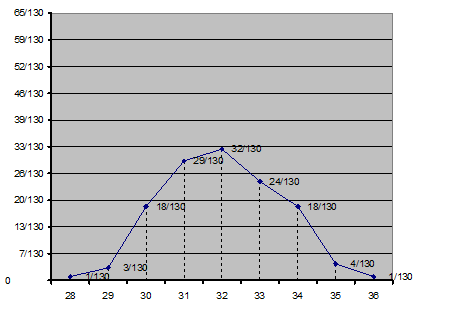
Построение эмпирической функции распределения

Статистическая функция распределения (эмпирическая) - это частота события, состоящего в том, что случайная величина Х в процессе изменения примет значение меньше некоторого фиксированного х

F^* (х) = Р^* = P^* (X<x)

Статистическая функция распределения (эмпирическая) является разрывной функцией, точки разрыва совпадают с наблюдаемыми значениями случайной величины, а скачок в каждой точке разрыва равен частоте появления наблюдаемого значения в данной серии наблюдения. Сумма скачков всегда равна 1.

9

Σ P_i * = 1

i=1

1) ∞ < х ≤ 28

F^* (x) =P^* (X<28) =0

2) 28<x≤29

F^* (x) =P^* (X<29) =P^* (X=28) =1/130

3) 29<x≤30

F^* (x) =P^* (X=28) + P^* (X=29) =1/130+3/130=4/130

4) 30<x≤31

F^* (x) =P^* (X<31) = P^* (X=28) + P^* (X=29) P^* (X=30) +1/130+3/130+18/130=22/130

5) 31<x≤32

F^* (x) =P^* (X<32) = P^* (X=28) + +P^* (X=29) +P^* (X=30) +P^* (X=31) =1/130+3/130+18/130+29/130=51/130

6) 32<x≤33