Курсовая работа: Комбінаторика

Інтервал ( x₀ – Е, x₀ + Е ), де Е > 0 називається Е – околом точки х₀ , при цьому точку х₀ називають центром, а число Е – радіусом околу. Цей окіл буде досить малий, якщо число Е теж буде мале.

Нехай задано дві множини А і В. Якщо кожен елемент множини А є елементом мнгожини В, то множину А називають підмножиною множини В і пишуть АВ (А міститься в В).

Наприклад N Z. Очевидно, що кожна множина є своєю підмножиною, а порожня множина є підмножиною будьякої множини.

Якщо множини А і В містять одні і ті ж елементи, тобто АВ і ВА, то їх називають рівними і пишуть А=В.

Множину, різні підмножини якої доводиться розглядати в процесі вивчення якогось питання, називають універсальною множиною.

У поцесі вивчення множин і функцій бувають корисними певні графічні зображення. У випадку множин застосовується діаграми Ейлера-Венна. На цих діаграмах схематично зображається універсальна множина у вигляді прямокутника, а різні підмножини універсальної множини у вигляді кругів.(мал.1.2).

А не має спільних елементів з В і С , а В і С мають спільні елементи.

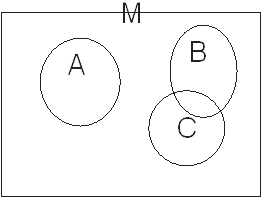
мал.1.2

§1. 2 Операції над множинами. Об’єднання і переріз двох множин.

Об’єданням двох множин А і В, називається множина А U В, елементи якої належать хочаб одній із цих множин.(мал.1.3)

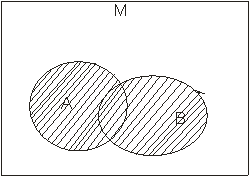
мал.1.3

Об’єдання декількох множин.

A_i = A₁ U A₂ U A₃ U…U A_n

A_i ={x | x є А₁ або х є А₂ або х є А₃ або …х є А_n }

Перерізом двох множин А і В називається множина А ∩ В елементи якої належать як і множині А, так і множені В. (мал.1.4)

А ∩ В={x | х є А і х є В}

A_i ={x | x є А₁ і х є А₂ , х є А₃ …х є А_n }

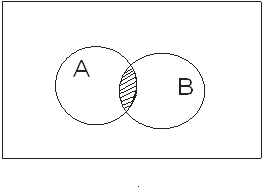
мал.1.4

Властивості об’єдання і перерізу множин:

Комутативний (переставний) закон

А U B = В U А;

А ∩ В = В ∩ А;

Асоціативний (сполyчний) закон.

А ∩ (В ∩ С) = (А ∩ В) ∩ С

А U (В U С) = (А U B) U С

Дистрибутивний (розподільний) закон.