Курсовая работа: Комбінаторика

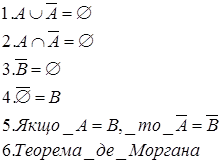
Для довільних підмножин А і В універсальної множини М, доповнення до множин А і В дорівнюють перерізу множин , а доповнення до перізу множин А і В дорівнює об’єднанню їх доповнень .

Доведемо цей закон за допогою діаграм Ейлера – Венна:

1) ||| = ||| =

||| =

мал.1.11 мал.1.12

2)

||| = ||| -

# =

мал.1.3 мал.1.4

Розділ 2. МНОЖИНИ З ВІДНОШЕННЯМ

§ 2. 1. Упорядковані пари. Прямий (декартів) добуток множин.

Множини {1,5} і {5,1}, що містять одні і ті ж самі елементи, рівні, причому запис порядку їх елементів не має значення. Проте, якщо розглядати на площині дві точки А (1,5) і В (5,1), то порядок запису їх координат (1 ; 5) має принципове значення. Можна навести і інші приклади, коли треба врахувати порядок розміщення елементів множини (вектор на площині, вектор у просторі). У зв’язку з цим вводиться поняття упорядкованої сукупності об ’ єктів, зокрема упорядкованої пари.

Упорядкована пара це двоелементна множина, елементи якої розміщені в певному порядку.

Якщо а є А і b є В, то пару утворену з цих елементів позначають (a; b).

Елемент а називають лівою (першою) координатою (компонентою) , а

b – правою (другою) координатою упорядкованої пари (а; b).

Множини А і В тут нерівноправні. При утворенні пари ставимо на перше місце елемент з А, а на друге – елемент з В. Припустимо, що користуючись таким правилом, ми утворили всі можливі пари, в яких на першому місці стоїть елемент з А, а на другому – з В. Множина всіх цих пар і називається прямим добутком.

Прямим (декартовим) добутком множин А і В називається множина усіх можливих пар, перші елементи яких належать множині А, а другій множині В і позначається А х В.

Отже, А х В = {(а; b)| а є А, b є В}

Декартів добуток множин не комутативний

А х В ≠ В х А

А х В = В х А лише тоді, коли А = В або одна із множин порожня.

Щодо асоціативного закону, то йому декарті добуток не підлягає навіть тоді, коли множини А, В і С рівні. Отже, якщо А ≠ Ш, то А х (А х А) ≠ (А х А) х А.

Для прямого добутку справедливі такі дистрибутивні закони:

(А В) х С = (А х С) (В х С)

А х (В С) = (А х В) (А х С)

(А ∩ В) х С = (А х С) ∩ (В х С)

А х (В ∩ С) = (А х В) ∩ (А х С)

А х (В \ С) = (А х В) \ (А х С)

Декартів добуток АхА називають декартовим квадратом і позначається

А І = А х А = {(a, b) | а є А, b є А}

Декартів добуток множин А, В, С визначається так само як і декартів добуток двох множин

А х В х С = {(a, b, с) | а є А, b є В, с є С}

Декарті добуток А х А х А називається декартовим кубом і позначається

А і = А х А х А

Якщо множину дійсних чисел R = (- ∞: + ∞) можна ототожнювати з числовою прямою, то декартів квадрат R х R дійсних чисел можна ототожнювати з числовою площиною. Очевидно, R х R – сукупність всіх можливих упорядкованих пар дійсних чисел (х; y).