Курсовая работа: Комбінаторика

А ∩ (В U С)=(А ∩ В) U (А ∩ С)

А U Ш = А.

А ∩ Ш = Ш.

Ці закони легко довести за допомогою діаграм. Доведемо 3-й дистрибутивний закон:

А U (В С) = (А U B) ∩ (А U С)

А U (В U С) (А U B) ∩ (А U С)

мал.1.5 мал.1.6

А ∩ (В U С)=(А ∩ В) U (А ∩ С)

А ∩ (В U С) (А ∩ В) U (А ∩ С)

мал.1.7 мал.1.8

§1. 3 Різниця і доповненя множин.

На відміну від об’єднання і перізу множин, операція віднімання визначається лише для двох множин якщо вони перетенаються.

Різницею множин А та В називається множина А\В, яка складається зусіх тих елементів, які належать множині А і не належать В.(мал.1.9)

А \ В = {x | x є A I x ў B}

мал.1.9

Властивості різниці :

· А \ В ≠ В \ А – не комутативна .

· А \ (В \ С) ≠ (А \ В) \ С – не асоціативна

· А U Ш = А.

· А ∩ Ш = Ш.

· (B U C) \ A=(B \ A) U (C \ A) – дисрибутивний закон віднімання відносно об’єдання;

· (B ∩ C) \ A = (B \ A) ∩ (C \ A) – дистрибутивний закон віднімання відносно перерізу;

Якщо А є В, то різницю В \ А називають доповненням множини А до множини В і записують - = В \ А

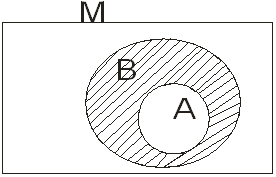
мал.1.10

Отже, доповненням до підмножини А в множину В називається множина всіх елементів із множини В, які не належать А