Курсовая работа: Комутаційні системи: принцип роботи, види та їх розрахунок

(12)

Умовні втрати для всіх викликів, що очікують:

(13)

Знайти умовні втрати для всіх поступивших і всіх очікуючих викликів для допустимого відносного часу очікування та

Умовні втрати для всіх викликів, що поступили:

при

при

Умовні втрати для всіх викликів, що очікують:

при

при

3.9 Розрахунок кількості точок комутації

Кількість точок комутації в напрямку в одноланковій повнодоступній схемі при обслуговуванні викликів найпростішого потоку комутаційною системою з очікуванням знаходимо за формулою:

Т1н = N * v. (14)

Кількість точок комутації в одноланковій повнодоступній схемі при обслуговуванні викликів найпростішого потоку комутаційною системою з очікуванням:

Т1 = N * M. (15)

Т1н = N * v=2320*143=3,318*10

4. РОЗРАХУНОК ОДНОЛАНКОВОЇ НЕПОВНОДОСТУПНОЇ КОМУТАЦІЙНОЇ СИСТЕМИ

4.1 Розрахунок за допомогою четвертої формули Ерланга

Неповнодоступна комутаційна схема – це схема з таким включенням виходів, при якому кожному входу доступні не всі, а лише частина виходів, хоча в сукупності всі входи можуть використовувати всі виходи. Для розрахунку одноланкової неповнодоступної схеми можна використати спрощений метод Ерланга. Якщо Y – питоме навантаження, яке поступає на повнодоступний пучок з’єднувальних ліній, v – число з’єднувальних ліній, які обслуговують це навантаження, D – доступність, р – імовірність втрат, то при малій імовірності втрат середня величина питомого навантаження, обслужного однією з’єднувальною лінією, буде приблизно рівна Y/v. Імовірність зайняття конкретної з’єднувальної лінії можна прийняти рівною середній величині питомого навантаження, обслуженого цією лінією. Імовірність зайняття D ліній рівна p= З цього співвідношення можна отримати v :

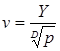(16)

z=1, бо система одноланкова

D=C1/z=C1=109