Курсовая работа: Комутаційні системи: принцип роботи, види та їх розрахунок

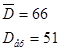
- навантаження, обслужене всіма D=51 лініями повнодоступного пучка при заданих втратах р(з першої формули Ерланга).

Умова v≤g *q*m виконується, бо 1361*3*55

5.2 Розрахунок за допомогою методу Якобеуса

Даний метод розрахунку двохланкових схем полягає в розв’язку системи рівнянь, запропонованої шведським вченим Якобеусом:

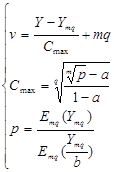(26)

де Cmax – максимальне навантаження на одну лінію;

Ymqн – навантаження, яке обслуговується повнодоступним пучком з mqн ліній.

Навантаження Ymqн визначається за першою формулою Ерланга при заданих втратах р і кількості ліній mqн .

– навантаження, яке обслуговується повнодоступним пучком з mqн=165 ліній(за першою формулою Ерланга).

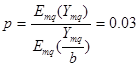
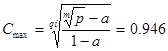
5.3 Розрахунок методом імовірнісних графів

Даний метод базується на представленні комутаційної системи у вигляді графа, конфігурація якого в загальному випадку залежить не тільки від структури схеми, але й від режиму пошуку, в якому використовується схема. Перехід від комутаційної системи практично будь-якої складності до графу не представляє особливих складностей. Граф являє собою картину всіх можливих шляхів між заданим входом системи і заданим виходом.

Процедура методу імовірнісних графів полягає в тому, щоб записати функцію для імовірності втрат при встановленні з’єднань в графі, що розглядається, між його вхідними і вихідними полюсами, аргументами якої є імовірності зайняття окремих дуг графа.

Нехай р1 – втрати проміжної лінії,

р1≈b≈a;ї

р2=Y/v

– втрати на вихідну лінію.

Тоді:

(1-р1) – імовірність того, що проміжна лінія вільна;

– втрати пучка ліній;

(1- – імовірність того, що пучок ліній вільний;

1-(1-р1)(1-р2) – імовірність зайнятості шляху.