Курсовая работа: Комутаційні системи: принцип роботи, види та їх розрахунок

4.2 Розрахунок за допомогою формули О’Делла

Згідно цього методу навантаження, обслужене повнодоступним пучком з v з’єднувальних ліній при імовірності втрат р, визначається як сума навантажень, обслужених повнодоступним пучком, який складається з D ліній, і неповнодоступним пучком, який містить v-D з’єднувальних ліній. Максимальне навантаження на одну з’єднувальну лінію визначається виразом:

(17)

де - навантаження, обслужене всіма D лініями повнодоступного пучка при заданих втратах р, Ерл.

Величина визначається за першою формулою Ерланга при заданих втратах р і кількості ліній D=С1. При вищевказаних вихідних даних навантаження YD можемо знайти за таблицями першої формули Ерланга.

-навантаження, обслужене всіма D=109 лініями повнодоступного пучка при заданих втратах р.

4.3 Розрахунок за допомогою формули Пальма-Якобеуса

В даному методі припускається, що процес зайняття з’єднувальних ліній в неповнодоступному пучку можна описати за допомогою розподілу Ерланга, отриманого ним для зайняття будь-яких D ліній в повнодоступному пучку. Вважаючи, що імовірність втрат в неповнодоступному пучку рівна імовірності зайняття D ліній, отримуємо наступний вираз для імовірності зайняття D ліній:

(18)

Для розрахунку використовується метод підбору і перша формула Ерланга.

При v=136

4.4 Розрахунок кількості точок комутації

Кількість точок комутації в напрямку в одноланковій неповнодоступній схемі:

Т1н=Nv/D, (19)

Кількість точок комутації в одноланковій неповнодоступній схемі:

Т1=ND. (20)

Т1н= Nv/D=2.575*10(v обчислине за четвертою формулою Ерланга)

Т1н= Nv/D=2.852*10 (v обчислине за формулою О’Делла)

Т1н= Nv/D=2.895*10(v обчислине за формулою Пальма-Якубеуса)

Т1=ND=2.529*10

5. РОЗРАХУНОК ДВОЛАНКОВИХ КОМУТАЦІЙНИХ СИСТЕМ

5.1 Розрахунок за допомогою методу ефективної доступності

Особливістю дволанкових комутаційних систем є те, що в з’єднанні між одним входом і одним виходом схеми крім точок комутації беруть участь також з’єднувальні лінії.

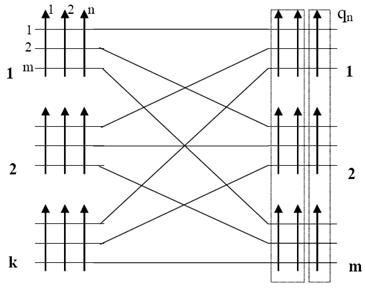
Рис. 1. Дволанкова комутаційна схема.