Курсовая работа: Критерии согласия
Пусть X – исследуемая случайная величина. Требуется проверить гипотезу H0 о том, что данная случайная величина подчиняется закону распределения F(x). Для этого необходимо произвести выборку из n независимых наблюдений и по ней построить эмпирический закон распределения F'(x). Для сравнения эмпирического и гипотетического законов используется правило, называемое критерием согласия. Одним из популярных является критерий согласия хи-квадрат К. Пирсона.
В нем вычисляется статистика хи-квадрат:
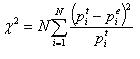 (2.1)
(2.1)
где N – число интервалов, по которому строился эмпирический закон распределения (число столбцов соответствующей гистограммы), i – номер интервала, pt i -вероятность попадания значения случайной величины в i-й интервал для теоретического закона распределения, pe i – вероятность попадания значения случайной величины в i-й интервал для эмпирического закона распределения. Она и должна подчиняться распределению хи-квадрат.
Если вычисленное значение статистики превосходит квантиль распределения хи-квадрат с k-p-1 степенями свободы для заданного уровня значимости, то гипотеза H0 отвергается. В противном случае она принимается на заданном уровне значимости. Здесь k – число наблюдений, p число оцениваемых параметров закона распределения.
Рассмотрим статистику:
![]() (2.2)
(2.2)
Статистика χ2 называется статистикой хи-квадрат Пирсона для простой гипотезы.
Ясно, что χ2 представляем собой квадрат некоего расстояния между двумя r-мерными векторами: вектором относительных частот (mi /n, …, mr /n) и вектором вероятностей (pi , …, pr ). От евклидового расстояния это расстояние отличается лишь тем, что разные координаты входят в него с разными весами.
Обсудим поведение статистики χ2 в случае, когда гипотеза Н верна, и в случае, когда Н неверна. Если верна Н, то асимптотическое поведение χ2 при n → ∞ указывает теорема К. Пирсона. Чтобы понять, что происходит с (2.2), когда Н неверна, заметим, что по закону больших чисел mi /n → pi при n → ∞, для i = 1, …, r. Поэтому при n → ∞:
![]() (2.3)
(2.3)
Эта величина равна 0. Поэтому если Н неверна, то χ2 →∞ (при n → ∞).
Из сказанного следует, что Н должна быть отвергнута, если полученное в опыте значение χ2 слишком велико. Здесь, как всегда, слова «слишком велико» означают, что наблюденное значение χ2 превосходит критическое значение, которое в данном случае можно взять из таблиц распределения хи-квадрат. Иначе говоря, вероятность Р(χ2 npi χ2 ) – малая величина и, следовательно, маловероятно случайно получить такое же, как в опыте, или еще большее расхождение между вектором частот и вектором вероятностей.
Асимптотический характер теоремы К. Пирсона, лежащий в основе этого правила, требует осторожности при его практическом использовании. На него можно полагаться только при больших n. Судить же о том, достаточно ли n велико, надо с учетом вероятностей pi , …, pr . Поэтому нельзя сказать, к примеру, что ста наблюдений будет достаточно, поскольку не только n должно быть велико, но и произведения npi , …, npr (ожидаемые частоты) тоже не должны быть малы. Поэтому проблема аппроксимации χ2 (непрерывное распределение) к статистике χ2 , распределение которой дискретно, оказалась сложной. Совокупность теоретических и экспериментальных доводов привела к убеждению, что эта аппроксимация применима, если все ожидаемые частоты npi >10. если число r (число различных исходов) возрастает, граница для npi можетбыть снижена (до 5 или даже до 3, если r порядка нескольких десятков). Чтобы соблюсти эти требования, на практике порой приходится объединять несколько исходов, т.е. переходить к схеме Бернулли с меньшим r.
Описанный способ для проверки согласия можно прилагать не только к испытаниям Бернулли, но и к произвольным выборкам. Предварительно их наблюдения надо превратить в испытания Бернулли путем группировки. Делают это так: пространство наблюдений разбивают на конечное число непересекающихся областей, а затем для каждой области подсчитывают наблюденную частоту и гипотетическую вероятность.
В данном случае к перечисленным ранее трудностям аппроксимации прибавляется еще одна – выбор разумного разбиения исходного пространства. При этом надо заботится о том, чтобы в целом правило проверки гипотезы об исходном распределении выборки было достаточно чувствительным к возможным альтернативам. Наконец, отмечу, что статистические критерии, основные на редукции к схеме Бернулли, как правило, не являются состоятельными против всех альтернатив. Так что такой метод проверки согласия имеет ограниченную ценность.
1.3 Критерии согласия для сложной гипотезы
На практике задача о согласии данных наблюдений с некоторым совершенно конкретным распределением, встречается реже, чем задача проверки сложной гипотезы, которую мы рассматриваем ниже.
Более трудной, но более важной для приложений задачей является проверка гипотезы о том, что данная выборка подчиняется определенному параметрическому закону распределения, например нормальному закону. Параметры этого закона остаются неопределенными, так что эта гипотеза сложная.
Пусть x1 , …, xn – выборка из распределения с функцией распределения
F(x, ![]() ). Здесь
). Здесь ![]() - неизвестный параметр, не обязательно скалярный.[11] Обозначим его истинное значение через
- неизвестный параметр, не обязательно скалярный.[11] Обозначим его истинное значение через ![]() º . Сейчас мы не можем сравнить выборочную функцию распределения Fn (x) и теоретическую, поскольку эта последняя нам не вполне известна: в ее выражение F(x,
º . Сейчас мы не можем сравнить выборочную функцию распределения Fn (x) и теоретическую, поскольку эта последняя нам не вполне известна: в ее выражение F(x, ![]() º ) входит неопределенный параметр
º ) входит неопределенный параметр ![]() º . Мы, однако, можем найти для
º . Мы, однако, можем найти для ![]() º приближенное значение, основываясь на выборке x1 , …, xn . Для этого можно использовать разные методы оценивания, но наиболее ясные и в определенном смысле наилучшие результаты получаются, если использовать метод наибольшего правдоподобия.
º приближенное значение, основываясь на выборке x1 , …, xn . Для этого можно использовать разные методы оценивания, но наиболее ясные и в определенном смысле наилучшие результаты получаются, если использовать метод наибольшего правдоподобия.
Итак, пусть ![]() n – оценка наибольшего правдоподобия по выборке x1 , …, xn для неизвестного параметра
n – оценка наибольшего правдоподобия по выборке x1 , …, xn для неизвестного параметра ![]() распределения F(x,
распределения F(x, ![]() ). Теперь для вычисления статистики Колмогорова вместо F(x,
). Теперь для вычисления статистики Колмогорова вместо F(x, ![]() º ) мы можем использовать F(x,
º ) мы можем использовать F(x, ![]() n ) и ввести модифицированную статистику Колмогорова:
n ) и ввести модифицированную статистику Колмогорова:
![]() (3.1)
(3.1)
Аналогично, модифицированная статистика омега-квадрат есть:
![]() (3.2)
(3.2)
Свойства статистик Dn и ![]() во многом повторяют отмеченные ранее свойства статистик Dn и
во многом повторяют отмеченные ранее свойства статистик Dn и ![]() . В частности,
. В частности, ![]() и n
и n![]() неограниченно возрастают, если проверяемая гипотеза неверна. Поэтому эту гипотезу следует отвергнуть, если наблюденное значение
неограниченно возрастают, если проверяемая гипотеза неверна. Поэтому эту гипотезу следует отвергнуть, если наблюденное значение ![]() (или n
(или n![]() , если применяется модифицированный критерий омега-квадрат) неправдоподобно велико, например, превосходит критическое значение, о котором будет сказано ниже.
, если применяется модифицированный критерий омега-квадрат) неправдоподобно велико, например, превосходит критическое значение, о котором будет сказано ниже.
Важно отметить, что статистика Dn распределена иначе, чем Dn (1.1), а статистика ![]() – иначе, чем
– иначе, чем ![]() (1.5). Причина в том, что из-за подбора
(1.5). Причина в том, что из-за подбора ![]() n по выборке функций F(x) и F(x,
n по выборке функций F(x) и F(x, ![]() n ) (в случае, если гипотеза о типе распределения верна) оказываются ближе к друг другу, чем F(x) и F(x,
n ) (в случае, если гипотеза о типе распределения верна) оказываются ближе к друг другу, чем F(x) и F(x, ![]() º ). Поэтому при справедливости гипотезы статистика Dn, как правило, будет принимать существенно меньше значения, чем Dn . Аналогично соотносятся
º ). Поэтому при справедливости гипотезы статистика Dn, как правило, будет принимать существенно меньше значения, чем Dn . Аналогично соотносятся ![]() и
и ![]() .
.
Поскольку статистики (3.1), (3.2) при справедливости гипотезы имеют иные распределения, чем статистики Dn и ![]() , для их применения необходимы таблицы распределений или хотя бы таблицы критических значений. К сожалению, модифицированные статистики (3.1), (3.2) не обладают столь привлекательным свойством «свободы от распределения выборки», как их прототипы, поэтому для каждого параметрического семейства распределений нужны свои таблицы. Более того, распределения (3.1), (3.2) могут зависеть и от истинного значения неизвестного параметра (параметров).[4] К счастью, для так называемых «масштабно-сдвиговых» семейств, к которым относятся нормальные, показательное и многие другие практически важные распределения, этого последнего осложнения не возникает.
, для их применения необходимы таблицы распределений или хотя бы таблицы критических значений. К сожалению, модифицированные статистики (3.1), (3.2) не обладают столь привлекательным свойством «свободы от распределения выборки», как их прототипы, поэтому для каждого параметрического семейства распределений нужны свои таблицы. Более того, распределения (3.1), (3.2) могут зависеть и от истинного значения неизвестного параметра (параметров).[4] К счастью, для так называемых «масштабно-сдвиговых» семейств, к которым относятся нормальные, показательное и многие другие практически важные распределения, этого последнего осложнения не возникает.
Таблицы распределений статистик (3.1), (3.2) к настоящему моменту составлены для многих семейств. Большинство из них рассчитаны методом случайных испытаний (методом Монте-Карло). Автор большинства этих расчетов М. Стефенс заметил, что зависимость результатов от объема выборки резко уменьшается, если вместо Dn , ![]() использовать их несколько преобразованные варианты. Стефенс утверждает, что для этих форм зависимость от n практически перестает сказываться, начиная с n = 5. ниже приводятся некоторые таблицы Стефенса.
использовать их несколько преобразованные варианты. Стефенс утверждает, что для этих форм зависимость от n практически перестает сказываться, начиная с n = 5. ниже приводятся некоторые таблицы Стефенса.