Курсовая работа: Критерии согласия

Чтобы не ломать бесплодно голову над вопросом, какими должны быть вероятности этих областей, а точнее в данном случае – их приближенные значения, возьмем их одинаковыми. Иными словами, в качестве границ интервалов используем решения уравнений

,

Замечу, что в качестве оценки функций распределения можно использовать и выборочную функцию распределения F_n (х), и другие возможности. В этом случае границами интервалов разбиения будут служить выборочные квантили (порядковые статистики).

После того, как мы определили интервалы разбиения числовой прямой, подсчитываем частоты т₁ , …, т_r , по которым будем вычислять потом статистику χ² (4.1) или (4.2) или какую- либо эквивалентную.

Следует подчеркнуть, что согласно теореме Фишера, для вычисления участвующих в этих формулах вероятностей р_і () следует использовать частоты т₁ , …, т_r , и только их. Никакой другой информацией пользоваться нельзя! Нельзя, например, использовать составлены по всей выборке ,а должны быть – по частотам т_і .

Можно даже сказать, какие последствия повлечет за собой нарушение этого запрета. Статистика χ² не будет (асимптотически) следовать распределению χ² с r – l степенями свободы (как было бы при точно известных параметрах). Ее функция распределения пройдет несколько выше. В качестве иллюстрации на рис. 4.1 приведе6м графики функций распределения хи-квадрат с 8, 10, 18 и 20 степенями свободы. Графики, соответствующие первым двум распределениям, выделяют область в которой будет проходить график функции распределения χ² при r = 11, если для вычисления р_і () использовались оценки . Последние два графика задают область нахождения функции распределения χ² при r = 21.

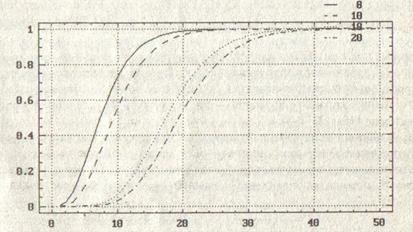
Рис. 4.1 функции распределения хи-квадрат с8,10,18 и 20 степенями свободы.

При больших r относительное развитие между квантилями распределений χ² с (r – 3) и (r – 1) степенями свободы невелико. Поэтому последствия такой ошибки не опасны. Но при r следует действовать «по теории».

Из-за всех этих сложностей, условий и оговорок можно сделать вывод, что для проверки гипотезы о нормальности выборки критерий Р. Фишера подходит плохо. Правильнее вместо этого использовать модификации критериев Колмогорова или омега-квадрат. Но для многих распределений вероятностей (например – дискретных) другой возможности, чем обсуждаемый критерий хи-квадрат Фишера, просто нет.

1.5 Другие критерии согласия. Критерии согласия для распределения Пуассона

Еще одна возможность для проверки согласия, которой тоже часто пользуются. Состоит она в том, что проверяют не исходную гипотезу целиком, а какие-либо ее последствие, которое считается важным. Для нормальной случайной величины ξ коэффициент асимметрии равен нулю.

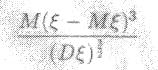(5.1)

Поэтому коэффициент асимметрии выборки

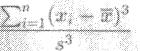(5.2)

тоже должен быть близок к нулю, если эта выборка – нормальная.

Чтобы судить о том, значимо ли отличается от нуля выборочное значение (5.2), и тем самым, не нарушено ли обязательное для нормального закона соотношение (5.1), надо знать, как распределена статистика (5.2) при гипотезе. Для малых выборок исследование подобных вопросов возможно далеко не всегда и, во всяком случае, требует особого рассмотрения в каждом случае. Иное дело большие выборки.

Есть стандартная методика, которая позволяет справится с этой задачей. Покажем ее действие на другом примере, поскольку о нормальном законе говорилось лишком много. Посмотрим, как можно проверить согласие выборки с распределением Пуассона. Для случайной величины ξ, распределенной по Пуассону

Dξ/Мξ = 1, (5.3)

так как для распределения Пуассона Dξ = Мξ = λ, где λ – параметр распределения. Поэтому если выборка х₁ , …, х_п извлечена из пуассоновской генеральной совокупности, то отношение должно быть близким к 1. Ниже пойдет речь о том как проверить.

(5.4)

Но сначала одно замечание общего характера: такие проверки никак не могут доказать соответствия выборки теоретическому закону даже при неограниченном возрастании числа наблюдений. Причина в том, что соотношение типа (5.1) и (5.3) не являются характеристиками: даже если (5.1) справедливо, оно не означает, что ξ непременно распределено нормально. Это свойство необходимо для нормальности распределения, но не достаточно. То же самое можно сказать о (5.3): это необходимое, но не достаточное условие для того, чтобы распределение было пуассоновским. После этого обсуждения обратимся к изучению свойств статистики (5.4). объем выборки п будет считать большим.

Воспользуемся тем, что при n → ∞ случайные величины S² – Dξ и х – Мξ стремятся к 0 (закон больших чисел). Поэтому для пуассоновской выборки:

Многоточие заменяет случайную величину, убывающую как n^-1 . раскрыв скобки, получаем, что:

Исследуем при n → ∞ поведение выражения