Курсовая работа: Критерій відношення правдоподібності для великих вибірок

Нехай випадкова величина і деяке дійсне значення. Тоді ймовірність того, що випадкова величина приймає значення менше за називається функцією розподілу ймовірностей випадкової величини і позначається Якщо функція розподілу залежить від деякого параметра , то писатимемо Клас функцій розподілу називатимемо класом допустимих розподілів спостережуваної випадкової величини і позначатимемо . Множина така, що і називається параметричною множиною. Той факт, що випадкова величина має функцію розподілу з класу будемо позначати і називати розподілом випадкової величини. Статистичною моделлю експерименту називається впорядкована пара де вибірковий простір випадкової величини клас розподілів цієї випадкової величини. Статистикою називають будь-яку випадкову величину, що залежить лише від вибірки . Статистика називається оцінкою невідомого параметра розподілу , якщо для кожної реалізації вибірки значення приймається за наближене значення параметра . Статистика називається незміщеною оцінкою параметра , якщо (тут - це математичне сподівання, тобто , якщо випадкова величина має неперервну функцію розподілу( у цьому випадку у точках існування похідної, і називається функцією щільності ), і у дискретному випадку( тобто набуває не більш, ніж зліченної кількості значень відповідно з ймовірностями , не більш, ніж зліченна множина і )). Позначимо через клас незміщених оцінок для параметра . Тоді, оптимальною оцінкою параметра називається така статистика , що

де і називається дисперсією випадкової величини .

Нехай щільність розподілу випадкової величини ( або ймовірність – у дискретному випадку), вибірка з розподілу ( тобто всі мають розподіл і є незалежними випадковими величинами), реалізація вибірки. Функція є щільністю розподілу випадкового вектора . Якщо розглядається при фіксованому значенні , то така функція параметра називається функцією правдоподібності. Оцінкою максимальної правдоподібності невідомого параметра називається таке значення , при якому для заданого .

Статистичною гіпотезою( або просто гіпотезою) називають будь-яке твердження щодо виду чи властивостей розподілу спостережуваної випадкової величини. Статистичні гіпотези надалі позначатимемо так: . Статистичною параметричною гіпотезою називається припущення про значення невідомого параметра розподілу Наведемо приклади параметричних гіпотез:

1)

2)

3) де взагалі кажучи, деяка векторна функція , стала.

Взагальному випадку параметрична гіпотеза задається деякою підмножиною , до якої, за припущенням, належить невідомий параметр . Тоді параметрична гіпотеза записується так: . Альтернативна гіпотеза має вигляд: ; точки називаються альтернативами. Якщо множина містить лише одну точку, то гіпотезу( альтернативу ) називають простою; у протилежному випадку гіпотезу( альтернативу) називають складною.

Правило, згідно якого висунута гіпотеза приймається або відкидається, називається статистичним критерієм( або просто критерієм) перевірки гіпотези .

Нехай вибірка з розподілу і висунута параметрична гіпотеза ( може бути як скаляром, так і вектором і надалі будемо вважати його вектором, якщо не обумовлено протилежне). Потрібно визначити чи узгоджується запропонована гіпотеза із результатами проведеного експерименту. У такому випадку поступають наступним чином: будують таке правило( критерій), яке дозволяє на основі отриманих реалізацій вибірки зробити висновок: прийняти гіпотезу чи відхилити її( прийняти альтернативу ). Отже, критерій розбиває вибірковий простір на дві множини такі, що , де складається із тих точок, для яких гіпотеза приймається, а множина із точок, для яких відхиляється. Множина називається областю прийняття гіпотези, а множина називається областю відхилення гіпотези, або критичною областю.

У процесі перевірки гіпотези можна прийти до правильного висновку або допустити помилку першого роду – відхилити , коли гіпотеза вірна, чи помилку другого роду – прийняти , коли вона хибна.

Ймовірності цих двох помилок можна виразити через функцію потужності критерію : . А саме: ймовірність похибки першого роду рівна , а ймовірність похибки другого роду рівна .

Число називають рівнем значущості критерію, якщо .

Нехай , тоді квантилем розподілу називається корінь рівняння . Якщо функція строго монотонна, то це рівняння має єдиний корінь; у протилежному випадку це рівняння має декілька коренів, і тоді квантилем називають мінімальний серед коренів рівняння.

2. Критерій відношення правдоподібності для великих вибірок

Одним із найбільш універсальних методів побудови критеріїв перевірки складних гіпотез є метод відношення правдоподібності, суть якого полягає у наступному. Для перевірки гіпотези проти альтернативи вводиться статистика відношення правдоподібності

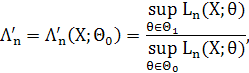
де , функція правдоподібності. Разом із статистикою вводиться статистика

Будемо вважати, що виконуються умови регулярності, що забезпечують існування, єдність і асимптотичну нормальність оцінки максимальної правдоподібності параметра . Розглянемо випадок простої гіпотези.

Теорема. Нехай потрібно перевірити просту гіпотезу фіксована внутрішня точка множини . Тоді для великих вибірок( ) при виконанні вказаних умов регулярності критерію відношення правдоподібності задається асимптотично критичною множиною

(1)

тобто при

де рівень значущості критерію.

Доведення. Покажемо, що з умов теореми слідує:

(2)

звідки випливає рівність (1). Якщо справедлива гіпотеза , то в силу спроможності оцінки максимальної правдоподібності при великих точка близька до , тому для можна записати розклад Тейлора відносно точки :