Курсовая работа: Критерій відношення правдоподібності для великих вибірок

Розглянемо декілька прикладів на застосування розглянутого критерію.

Приклад 1. Кількість бракованих деталей у партії не повинна перевищувати . У результаті контролю 100 деталей із цієї партії виявлено 6 бракованих. Чи можна вважати, що відсоток браку рівний при ?

Розв’язання. Для розв’язку задачі застосуємо критерій відношення правдоподібності для великих вибірок. Нехай ймовірність браку деталі, ймовірність того, що деталь справна,. - припущення про параметр розподілу. Отже, перевіримо просту гіпотезу , тоді альтернативна гіпотеза тут У нашому випадку , тоді статистика критерію

Для заданого рівня значущості знаходимо критичну точку ( див. Додаток А). Отже, отримали, що при даній реалізації вибірки статистика критерію отримала значення , яке менше критичного значення , тобто гіпотеза приймається, а тому відсоток браку можна вважати таким, що рівний .

Приклад 2. Гральний кубик підкинули 600 разів, при цьому шестірка випала 75 разів, п’ятірка – 118, четвірка – 124, трійка – 108, двійка – 92 і одиничка - 83. Чи можна вважати, що кубик симетричний і однорідний? Прийняти

Розв’язання. У цій задачі невідомий параметр, причому , Тоді . Гіпотеза , альтернатива . Знайдемо значення статистики критерію

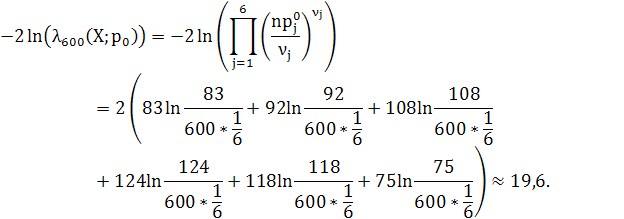
Критична точка . Оскільки, то гіпотеза відхиляється, тому не можна вважати, що кубик симетричний і однорідний.

Приклад 3. Метод одержання випадкових чисел був застосований 250 разів, при цьому отримали наступні результати:

Цифра	0	1	2	3	4	5	6	7	8	9
Частота появи	27	18	23	31	21	23	28	25	22	32

Чи можна вважати, що застосований метод дійсно генерує випадкові числа? Покласти Розв’язання. Згідно умови задачі, невідомий параметр, , Тоді . Гіпотеза , альтернатива . Знайдемо значення статистики критерію:

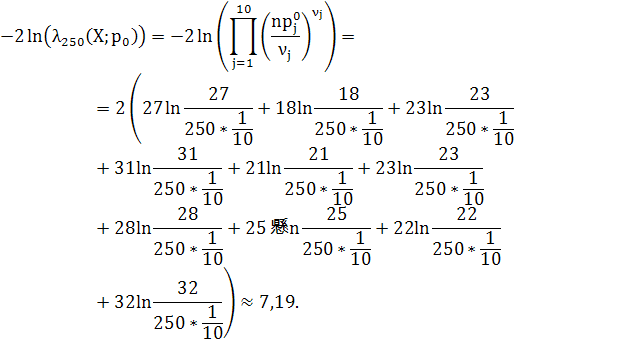
Критична точка множини . Отже, , тому гіпотеза приймається. Тому можна вважати, що застосований метод справді генерує випадкові числа.

4. Опис програми

Призначення програми. Використовуючи програму, код модуля якої наведений у додатку B, можна розв’язувати задачі на узгодженість простої параметричної гіпотези із реалізаціями великих вибірок. Перевірка узгодженості проводиться на основі критерію відношення правдоподібності для великих вибірок.Умови застосування. Програма коректно працює на IBM – сумісних комп’ютерах з такими характеристиками: Celeron 2.26/MBASUSP4VM-800 /DDR 1.5GbPC3200/ HDD 330 Gb 7200 rpm/ Radeon 9250 128/128, під операційною системою – WindowsXPProfessionalSP3 із встановленим програмним забезпеченням – середовищем розробки - Delphi 7.

Опис задачі та вихідні дані. У додатку Cнаводяться три результати виконання програми.У першому випадку при вводі даних вручну потрібно вказати у відповідні поля кількість різних значень випадкової величини та рівень значущості. У таблицю вводяться частоти і ймовірності, з якими випадкова величина набуває відповідні значення.У другому випадку розглядається подібна задача, тільки тут дані зчитуються з файлу.У третьому випадку програма сама генерує вибірку з нормального розподілу і перевіряється гіпотеза про значення математичного сподівання і дисперсії цього розподілу, причому на формі вказується значення математичного сподівання, дисперсії і рівня значущості.Текст програми. У додатку B наведений код модуля програми, оскільки при написанні програми використано візуальне середовище Delphi 7.Результати. У додатку Cнаведені результати виконання програми на різних контрольних прикладах.

Висновки

У курсовій роботі було розглянуто один із критеріїв відношення правдоподібності, а саме: критерій відношення правдоподібності для великих вибірок, його теоретичне обґрунтування, застосування до розв’язування практичних задач. Проте, як і будь-який інший статистичний критерій, він має свої переваги і недоліки, які визначають його практичну цінність. Тому розглянемо їх.

Критерії відношення правдоподібності мають широке практичне застосування з огляду на такі їхні властивості( які мають місце у широкому класі задач), як:

1. Критерії відношення правдоподібності є найбільш потужними серед усіх інших можливих критеріїв( лема Неймана - Пірсона).

2. Щільність розподілу критичної статистики можна легко отримати із функції правдоподібності спостережуваної випадкової величини( у випадку застосування цих критеріїв до перевірки гіпотез для великих вибірок, користуються асимптотичною щільністю хі -квадрат розподілу).

Однак, варто відзначити, що ці критерії мають ряд недоліків, які дещо звужують коло застосувань цих методів. Одним із головних недоліків є вимога регулярності функцій правдоподібності, що не завжди має місце на практиці. Інші два недоліки мають місце при застосуванні будь-яких статистичних критеріїв. Це так звані ефекти "надто малого об’єму вибірки" та ефекти "надто великого об’єму вибірки".

Ефект " надто малого об’єму вибірки" полягає у тому, що при заданому рівні значущості критерію і малій кількості спостережень( ), на основі яких отримують потужність критерію, тобто ймовірність відхилити нульову гіпотезу у випадку, коли вона насправді хибна, є дуже малою. У такому випадку застосовують два підходи: або дещо збільшують значення рівня значущості критерію ( що, у свою чергу, призводить до зменшення похибки другого роду, але одночасного збільшення похибки першого роду), або збільшують об’єм вибірки .

Ефект "надто великого об’єму вибірки" полягає у тому, що при великих значеннях надзвичайно сильно зростає чутливість критерію до емпіричних результатів, і в таких випадках висунута гіпотеза практично завжди відхиляється критерієм. Для того, щоб уникнути ефекту великої вибірки, апріорне визначення характеристик критерію( рівня значущості і похибки другого роду ) потрібно пов’язувати з об’ємом вхідних даних . Виграш у чутливості критерію, який отримується при зростанні , доцільно використати для зменшення як , так і . Зокрема, якщо при збільшенні зменшувати , то дуже малі відхилення від вже не приведуть до обов’язкової неузгодженості з емпіричними даними: ймовірність цього факту буде залежати від того, з якою швидкістю зменшується при зростанні .

Список використаної літератури

1. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. Справочное пособие. – М.: Финансы и статистика, 1983. – 471 с.

2. Ефимов А.В. Сборник задач по математике для втузов. Специальные курсы. Т.3. – М.: Наука, 1984. – 608с.

3. Ивченко Г.И., Медведев Ю.И. Математическая статистика. – М.: Высш. шк., 1984. – 248с.

4. Ружевич Н.А. Математична статистика. – Львів: Львівська політехніка, 2001. – 168 с.