Курсовая работа: Линейные диофантовы уравнения

имеет решение в целых числах. , очевидно, не пусто, так как при заданных , можно подобрать целые значения , такие, чтобы было положительным числом.

В множестве существует наименьшее число ( – подмножество натуральных чисел), которое мы обозначим через Обозначим через - целые числа, такие, что

.

Пусть , где ; тогда

.

Мы подобрали целые значения: , ,…, , такие, что , но , а - наименьшее положительное число в , т. е. не может быть положительным, , , .

Аналогично получаем: ,…,.

Мы видим, что – общий делитель чисел , следовательно, поскольку , , , , то уравнение разрешимо в целых числах.

Теорема 2. Пусть - наибольший общий делитель коэффициентов . Диофантово уравнение имеет решение тогда и только тогда, когда . Число решений такого уравнения равно либо нулю, либо бесконечности.

Докажем последовательно все три утверждения теоремы.

1). Пусть . Для уравнения

,

где 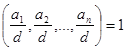, существуют целые числа: удовлетворяющие ему. Т.е. такие, что

.

Тогда

т. е. - решение уравнения.

2). Пусть теперь не делит . Тогда левая часть уравнения при любых целых делится на , а правая на не делиться, так что равенство при целых значениях невозможно.

3). Если - упорядоченная n-ка чисел, удовлетворяющий уравнению, то например, все n-ки

при

также удовлетворяют этому уравнению и, таким образом, у нас либо совсем не будет решений, либо их будет бесконечное множество.

Если хоть одна пара коэффициентов взаимно простая, то , и уравнение имеет бесчисленное множество решений.

3. Нахождение решений для некоторых частных случаев ЛДУ.

3.1. ЛДУ c одной неизвестной.

Рассмотрим линейное уравнение с одной неизвестной, т.е. уравнение вида

Ясно, что решением данного уравнения будет , и решение будет целым числом только в том случае, когда .

3.2. ЛДУ с двумя неизвестными.

Рассмотрим теперь линейное уравнение с двумя неизвестными

, .