Курсовая работа: Линейные диофантовы уравнения

перейдем к равносильному уравнению

(*),

где. Пусть, - два ненулевых числа, таких, что Для определенности предположим, что, Разделив с остатком на , получим представление . Заменив на в уравнении (*), приведем его к виду

Перепишем это уравнение в виде

(**)

где

, .

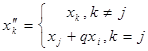Очевидно, что решения уравнения (*) и (**) связаны между собой взаимно однозначным соответствием и, таким образом, решив уравнение (**), несложно найти все решения уравнения (*). С другой стороны отметим, что

Отметим также, что

Следовательно, за конечное число шагов уравнение (*) приведется к виду

(***)

где числа (i = 1,...,n), которые не равны нулю, равны между собой по абсолютной величине. Из соотношения следует, что числа могут принимать только значения 0,±1, причем не все из них равны нулю. Предположим, для определенности, . Тогда уравнение (***) имеет следующее решение:

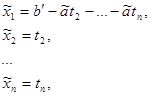
где t2, t3, ..., tn - произвольные целые числа. Отсюда, учитывая проведенные замены, получается и решение уравнения (*). Отметим, что при получении решения уравнения (***) использовался лишь факт, что , поэтому, при выполнении алгоритма можно остановиться на том шаге, когда хотя бы один из коэффициентов станет равным ±1.

5. Примеры решений задач.

1). Решить в целых числах уравнение

4x - 6y + 11z = 7, (4,6,11)=1.

Разделив с остатком -6 на 4, получим -6 = 4(-2) + 2. Представим исходное уравнение в виде

4(x - 2y) + 2y + 11z = 7.

После замены x = x - 2y это уравнение запишется следующим образом

4x + 2y + 11z = 7.

Учитывая, что 11 = 2·5 + 1, преобразуем последнее уравнение:

4x + 2(y + 5z) + z = 7.

Положив y = y + 5z, получим

4x + 2y + z = 7.