Курсовая работа: ЛИСП-реализация основных способов вычисления гамма-функции

или после изменения в правой части порядка интегрирования ,получаем:

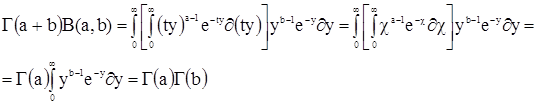
откуда

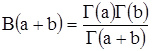(2.2)

заменяя в (2,1) , на и интегрируем по частям

получаем рекурентною формулу

(2.3)

так как

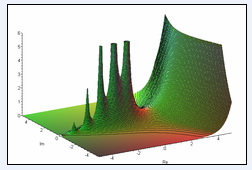
Рисунок 2. График модуля гамма-функции на комплексной плоскости

При целом имеем

(2.4)

то есть при целых значениях аргумента гамма-функция превращается в факториал, порядок которого на единицу меньше взятого значения аргумента. При n=1 в (2.4) имеем

2.2 Вычисление гамма функции

Для вычисления гамма-функции используется аппроксимация логарифма гамма-функции. Сама же гамма вычисляется через него.

Для аппроксимации гамма-функции на интервале x>0 используется формула (для комплексных z) такого вида:

.

Она похожа на аппроксимацию Стирлинга, но в ней имеется корректирующая серия. Для значений g=5 и n=6, проверено, что величина погрешности eps не превышает . Кроме того, погрешность не превышает этой величины на всей правой половине комплексной плоскости: Re z > 0.

Для получения действительной гамма-функции на интервале x>0 используется рекуррентная формула Gam(z+1)=z*Gam(z) и вышеприведенная аппроксимация Gam(z+1). Также можно заметить, что удобнее аппроксимировать логарифм гамма-функции, чем ее саму.

Во-первых, при этом потребуется вызов только одной математической функции – логарифма, а не двух – экспоненты и степени (последняя все равно использует вызов логарифма), во-вторых, гамма-функция – быстро растущая для больших x, и аппроксимация ее логарифмом снимает вопросы переполнения.

Для аппроксимации LnGam() – логарифма гамма-функции – получается формула:

Значения коэффициентов C_k являются табличными данными (Таблица 1).

k	C
1	2.5066282746310005
2	1.0000000000190015
3	76.18009172947146
4	-86.50532032941677
5	24.01409824083091
6	-1.231739572450155
7	0.1208650973866179e-2
8	-0.5395239384953e-5

Таблица 1. Значения коэффициентов C_k

Сама гамма-функция получается из ее логарифма взятием экспоненты. .

3 Функциональные модели и блок-схемы решения задачи