Курсовая работа: ЛИСП-реализация основных способов вычисления гамма-функции

;ПРИМЕНЯЕМДЛЯПОЛОЖИТЕЛЬНЫХЧИСЕЛ

(PRINT (MAPCAR 'GAMMA FUNC) OUTPUT_STREAM)

;ПРИМЕНЯЕМДЛЯПОЛОЖИТЕЛЬНЫХЦЕЛЫХЧИСЕЛ

(PRINT (MAPCAR 'GAMMA_WHOLE FUNC) OUTPUT_STREAM)

;ПРИМЕНЯЕМДЛЯЛЮБЫХЧИСЕЛ

(PRINT (MAPCAR 'GAMMA_POINT FUNC) OUTPUT_STREAM)

(TERPRI OUTPUT_STREAM)

(CLOSE OUTPUT_STREAM)

;END

5 Пример выполнения программы

Пример 1.

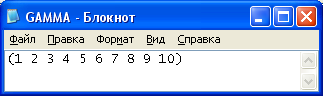
Рисунок 7 – Входные данные. Вычисление гамма-функции для положительных целых чисел

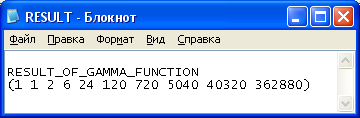
Рисунок 8 – Выходные данные. Вычисление гамма-функции для положительных целых чисел

Пример 2.

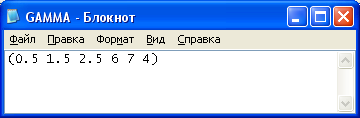
Рисунок 9 – Входные данные. Вычисление гамма-функции для положительных чисел

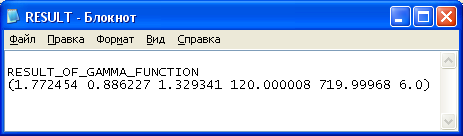
Рисунок 10 – Выходные данные. Вычисление гамма-функции для положительных чисел

Пример 3.

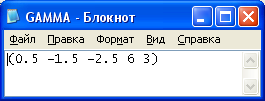
Рисунок 11 – Входные данные. Вычисление гамма-функции для множества чисел

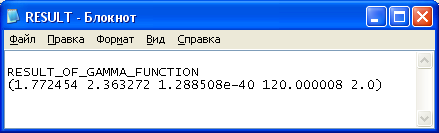
Рисунок 12 – Выходные данные. Вычисление гамма-функции для множества чисел

ЗАКЛЮЧЕНИЕ

Гамма функции являются удобным средством для вычисления некоторых интегралов в частности многих из тех интегралов, которые не представимы в элементарных функциях. Благодаря этому они широко применяются в математике и ее приложениях, в механике, термодинамике и в других отраслях современной науки.

Итогом работы можно считать созданную функциональную модель реализации основных способов вычисления гамма функции. Данная модель применима к гамма-функции с положительным целым параметром, гамма-функции с положительным параметром, гамма-функции для множества точек. Созданная функциональная модель реализации основных способов вычисления гамма функции и ее программная реализация могут служить органической частью решения более сложных задач.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы