Курсовая работа: Математическое моделирование технических объектов

2.2.2Cхема сайта
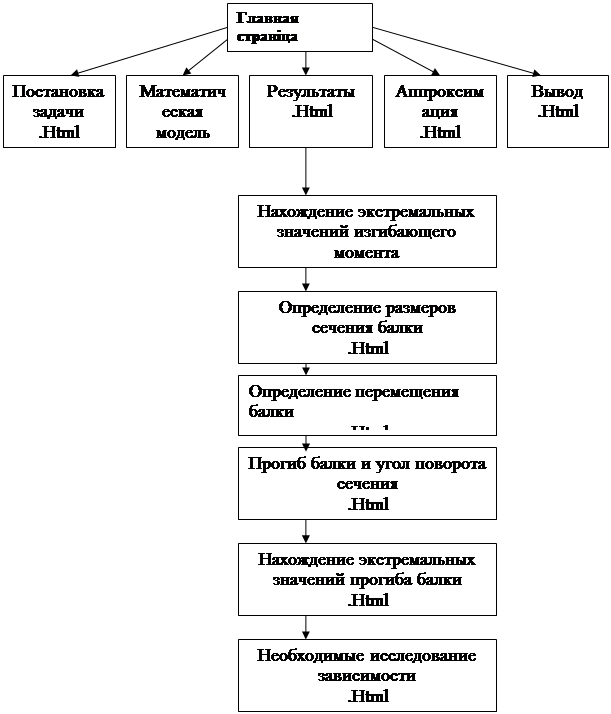
3 Описание документа MathCad
3.1 Система MathCad
MATHCAD - естественный математический язык, на котором формируются решаемые задачи. Объединение текстового редактора с возможностью использования общепринятого математического языка. Позволяет пользователю получить готовый итоговый документ. Пакет обладает широкими графическими возможностями, расширяемыми от версии к версии. Практическое применение пакета существенно повышает эффективность интеллектуального труда. Особенности MATHCAD состоят в том, что он не только позволяет провести необходимые расчеты, но и оформить свою работу с помощью графиков, рисунков, таблиц и математических формул. Возможности системы объединяет в себе простой текстовый редактор, математический интерпретатор и графический процессор.Текстовый редактор системы не обладает всеми возможностями специализированных редакторов текста, однако позволяет корректировать тексты, выравнивать их по краю, перемещать текстовые блоки в любое место документа и т.д. Математический интерпретатор системы - наиболее интересная её часть. Математические формулы, подлежащие интерпретации, записываются в общепринятом виде.
3.2 Таблица используемых переменных
| Символьное обозначение |
Единицы измерения | Расшифровка величины |
| L | метр | Длина участка |
| P | ньютон | Сила |
| Q | Н/м | Распределённая нагрузка |
| σ | Н/м2 | Допустимое напряжение |
| E | Н/м2 | Модуль упругости |
| Ra | Н | Опорная реакция |
| M | J | Изгибающий момент |
| W | J | Минимальный осевоймомент инерции |
| d | м | Диаметр балки |
| j | м4 | Момент инерции |
| Ra1 | Н | Реакция от единичной нагрузки |
| Ra2 | Н | Момент реакции от единич. момента |
| ∆(xx) | м | Прогиб балки |
| (xx) | Угол поворота сечения |
4. Необходимые исследования зависимостей в MathCad
Для исследования зависимости диаметра балки от P3, необходимо, каждый раз в новом окне MathCad, равномерно изменять значения силы P3 и соответственно полученные значения диаметра балки d.
Аналогично находим зависимости максимального прогиба балки от L4, для этого изменяем значения длины L4 и полученные при этом значения максимального прогиба балки.
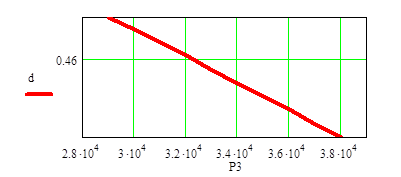
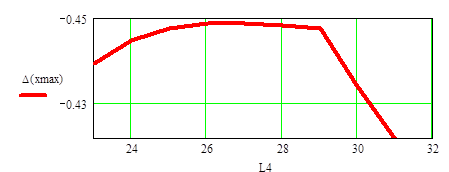
Строим график зависимости силы P3 от диаметра балки d, а также длины L4 от максимального прогиба балки.
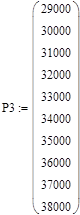
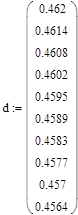
где:
- P3 – сила, действующая на балку;
- d – диаметр балки
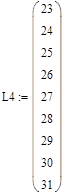
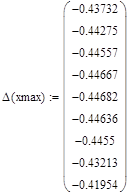
где:
- L4 – длины участка;
- ∆(xmax) –максимальный прогиб балки
5. Аппроксимация
Находим аппроксимирующую функцию для зависимости диаметра балки от P3. Для этого нам необходимо определить набор функций с помощью которых будем аппроксимировать. Воспользуемся встроенной функцией linfit для определения вектора коэффициентов аппроксимирующей функции. Построить график.
Аналогично для зависимости максимальный прогиб балки от L4
Определяем набор функций с помощью которых будем аппроксимировать

Определяем вектор коэффициентов аппроксимирующей функции