Курсовая работа: Математическое моделирование тепловой работы вращающейся печи

С помощью уравнений, полученных на основе теории турбулентных струи, вычисляют основные параметры диффузионного факела: длину факела; массовый расход воздуха, вовлеченного в струю; массовый расход несгоревшего топлива; энтальпию газообразной среды, усредненную по сечению струи и среднюю по сечению температуру диффузионного факела.

Для вычисления средней плотности газообразной среды предлагается следующий итерационный алгоритм. Разделим факел по длине на достаточно малые участки, в пределах которых температуру и плотность среды можно считать постоянными. Например, удобно принять длину такого участка ∆х равной диаметру выходного отверстия горелки d₀ .

Примем в качестве расчетного поперечное сечение факела на выходе из очередного малого участка. Температура, состав и плотность газов на входе в очередной малый участок известны как параметры в предыдущем поперечном сечении, так что, приняв эти величины в качестве расчетных, можно получить в первом приближении массу воздуха, присоединенного к струе на очередном малом участке за единицу времени:

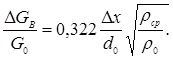
где - средняя плотность газов на очередном малом участке.

Прибавим эту величину к массовому расходу воздуха, вовлеченного в движение струи перед очередным малым участком, и найдем его массовый расход в расчетном сечении:

Массовому расходу воздуха G_в , в уравнении соответствует средняя плотность среды на расчетном участке от горелки до расчетного сечения:

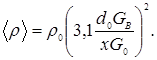
Теперь можно определить расстояние от горелки до полюса струи, расчетную длину факела, массовый расход несгоревшего топлива, энтальпию и температуру факела в расчетном сечении; а затем, не меняя значения координаты X, уточнить среднюю плотность среды на очередном малом участке.

Плотность среды на расчетном участке и температуру среды в расчетном сечении вычисляют повторно, каждый раз уточняя величину ρ_{с p} , пока не будет достигнута заданная точность результатов. После этого увеличивают координату X на приращение ∆х, равное длине очередного малого участка, и выполняют расчет параметров диффузионного факела в следующем расчетном сечении в пределах участка струйного течения.

Алгоритм расчета температуры футеровки печи

Температурное поле в поперечных сечениях футеровки печи рассчитывают по уравнениям. Так как допускается пренебрегать переносам теплоты в футеровке по длине печи и цилиндричностью стенок, то становится возможной постановка одномерной задачи в декартовой системе координат.

Рекомендуется сначала составить более простую программу расчета стационарной теплопроводности при граничных условиях первого рода на внутренней поверхности футеровки. В начале программы выполняется цикл по индексу j для вычисления координат узлов сетки:

где ∆у – расстояние между узловыми точками, определяемое по заданной толщине футеровки и выбранному числу узлов сетки:

Затем температуру на внутренней поверхности футеровки приравнивают к температуре технологического материала и задают произвольные исходные значения температуры в остальных узловых точках.

В общем итерационном цикле последовательно увеличивают на единицу номера итераций N, вычисляют коэффициент теплопроводности материала футеровки и, выполняя прямую прогонку, рассчитывают коэффициенты прогонки Рj, Sj. Затем, вычислив коэффициенты дискретного уравнения, находят температуру на наружной поверхности футеровки в соответствии с граничными условиями третьего рода. Степень черноты наружной поверхности футеровки вращающейся печи принимают равной 0,9. Выполняя обратную прогонку, находят значения температуры во внутренних узлах сетки.

Температуру в пределах программы следует выражать в кельвинах. Так как коэффициенты теплопроводности футеровки вычисляются в точках, лежащих на гранях контрольных объемов между узлами сетки, то в расчетные формулы подставляют среднеарифметические значения температуры в соседних узловых точках:

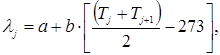
где а, b– числовые коэффициенты.

Согласно принятой здесь нумерации точек на гранях контрольных объемов, формулы для расчета коэффициентов дискретных уравнений будут представлены следующим образом:

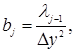
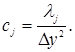
Коэффициент теплопроводности слоя гарнисажа, образованного на внутренней поверхности футеровки застывшим клинкерным расплавом, принимают равным 1 Вт/(м•К).

В цикле обратной прогонки вычисляют в узлах сетки относительные разности значений температуры в текущей и предыдущей итерациях:

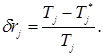
и выбирают из них максимальную разность. В конце общего итерационного цикла производят оценку сходимости итераций, сравнивая абсолютную величину с заданным малым числом. Если || больше чем, например, 0,00001, то итерации повторяются, если же меньше, то итерации завершаются. Чтобы повторить вновь выбор максимальной относительной разности температур, в начале каждой итерации величину устанавливают равной нулю.

В конце программы предусматривают вывод на экран и на печать исходных данных и результатов расчета. При этом температуру представляют в градусах Цельсия.