Курсовая работа: Математическое моделирование тепловой работы вращающейся печи

Коэффициенты прогонки Рj, Sjна внутренней поверхности футеровки или гарнисажа определяют теперь, предварительно вычислив коэффициенты дискретного уравнения. При этом используются значения степени черноты и поглощательной способности газообразной среды, приведенной степени черноты и коэффициента конвективной теплоотдачи, найденные при расчете параметров диффузионного факела. Температуру на внутренней поверхности футеровки или гарнисажа определяют обратной прогонкой.

Третью программу составляют для расчета нестационарного теплообмена, имея в виду, что при вращении печи температура внутренней поверхности футеровки изменяется. При контакте с технологическим материалом она равна температуре этого материала, что соответствует граничным условиям первого рода, а при нагреве диффузионным факелом зависит от условий радиационной и конвективной теплоотдачи, согласно граничным условиям третьего рода.

Для учета нестационарности в программе организуют цикл по интервалам времени, который является внешним по отношению к итерационному циклу. Цикл по интервалам времени выполняется в течение нескольких оборотов печи, так чтобы расчетное время прогрева футеровки оказалось достаточным для стабилизации изменений температурного поля в следующих друг за другом оборотах.

Чтобы задать начальное температурное поле в футеровке, целесообразно усреднить стационарные распределения температуры, полученные в двух предыдущих программах при граничных условиях первого и третьего рода. По-прежнему допускается рассматривать задачу приближенно как одномерную. Коэффициент aj, Dj дискретных уравнений рассчитывают теперь с учетом нестационарных членов.

Окружность печи делят на 16, расчетных отрезков и определяют интервал времени, необходимый для прохождения каждого отрезка расчетным сечением футеровки при вращении печи

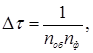
где n_об – частота вращения печи (1/с).

Если расчетный отрезок футеровки находится под слоем технологического материала, в программе используются граничные условия первого рода. Для остальных участков футеровки расчет выполняется при граничных условиях третьего рода.

Чтобы выделить интервалы времени, когда футеровка находится под слоем технологического материала, разделим порядковый номер расчетного интервала времени на число расчетных отрезков по окружности печи. Те расчетные моменты времени, для которых величина получаете целой, соответствуют началу нового оборота печи. На первом обороте печи это начальный (нулевой) момент времени, а на остальных оборотах печи это моменты времени, порядковые номера которых кратны числу n_ф .

Если расчетным отрезкам по окружности футеровки, находящимися под слоем технологического материала, присвоить порядковые номера, то соответствующие им расчетные моменты времени можно определить из условия, что отношение , является целым числом.

Поперечное сечение вращающейся печи:

1-футеровка; 2 – слой гарнисажа; 3 – технологический материал.

Программа №1

Program Kurs;

{Математическое моделирование тепловой работы вращающейся печи}

uses Crt;

const SI = 5.67e-8; {Постоянная Стефана-Больцмана, Вт/(м2*К4)}

SC = 0.85; {Турбулентное число Шмидта}

type tFurnace = object

X: integer;

Dk, Dw, D0, Hw, Hw1, Tm, Ew1, Ew2: real;

X0, RF, FR, LF, AG, ES, EG: real;

BT, G0, R0, U0, H0, QT, GT: real;

GB, GB0, ROB, TB, HB: real;

ALB, NB, VB0, V1, V2, V3, VG0: real;

TF, TK, TP, QF, QP, HF: real;

Cg, Cv, CF, ROF, ROV, RO: real;

P1, P2, P3, PT, PG, PB: real;