Курсовая работа: Метод Галеркіна пошуку розв’язку лінійної крайової задачі

Самі додаткові умови можуть зв’язувати між собою значення кількох функцій в одній точці (або навіть в різних точках); тоді для системи р-го порядку вони приймуть вигляд

,

, .

Існують задачі з ще більш складнішими за формою крайовими умовами, наприклад, умовами нормування

,

звичними в квантовій механіці, і т. д.

Не дивлячись на різноманітність форм крайових умов, крайові задачі розв'язуються в основному одними і тими ж чисельними методами, що виправдовує їх об'єднання в один тип. Зупинимося на методах розв’язування.

Знайти точний роз’язок крайової задачі в елементарних функціях вдається рідко: для цього треба знайти загальний розв’язок системи (1) і зуміти явно визначити з крайових умов значення сталих, що входять у нього.

До наближених методів розв’язку крайових задач відносяться розклад в ряди Фур’є, методи Рітца і Галеркіна. Ряди Фур’є застосовуються до лінійних задач. Інші два методи застосовуються і до деяких нелінійних задач.

Для чисельного розв’язку крайових задач використовують метод стрільби і різницевий метод. Метод стрільби базується на зведенні крайової задачі до деякої задачі Коші для тієї ж системи рівнянь. В різницевому методі задача наближено заміняється розв’язком алгебраїчної системи рівнянь з досить великим числом невідомих. У випадку нелінійних задач обидва методи є ітераційними; при цьому побудова ітераційних процесів, що добре збігаються, виявляється достатньо складною.

М атематична модель задач і

Методи приблизного розв’язання поставлених крайових задач можна розбити на дві групи: різницеві методи і аналітичні методи. До різницевих методів розв’язку лінійної крайової задачі відносять: метод скінченних різниць для лінійних диференціальних рівнянь другого порядку, метод прогонки. До аналітичних методів – метод Галеркіна, метод колокацій.

Метод скінченних різниць дозволяє знайти наближений розв’язок крайової задачі у вигляді таблиці, а аналітичні методи дають можливість знайти наближений розв’язок лінійної крайової задачі у вигляді аналітичного виразу. Розглянемо метод Галеркіна для знаходження наближеного розв’язку лінійної крайової задачі.

Метод Галеркіна базується на одній теоремі з теорії загальних рядів Фур’є.

Теорема. Нехай - повна система функцій з ненульовою нормою, ортогональних на відрізку [a, b]. Якщо неперервна функція ортогональна на відрізку [a, b] до всіх функцій , тобто

(n=0, 1, 2, . . .), (3)

то при

Доведення. Розглянемо ряд Фур’є функції відносно заданої системи ортогональних функцій

(4)

Як відомо, коефіцієнти Фур’є визначаються за формулою

де

В силу умови (3) маємо

(n = 0, 1, 2, . . .). (5)

Для повної системи у відношенні до будь-якої неперервної функції виконана рівність повноти

(6)

Звідси, враховуючи рівність (5), маємо

і, отже, при

Зауваження. З формули (4) випливає, що якщо неперервна функція

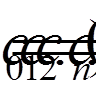ортогональна до кінцевої системи функцій (тобто то

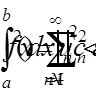
при достатньо великому N. В цьому випадку функція в середньому на відрізку [a, b] буде як завгодно малою. При додаткових обмеженнях звідси випливає, що 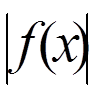також малий на відрізку

Перейдемо до викладу метода Галеркіна. Нехай маємо лінійну крайову задачу

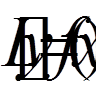(7)

де 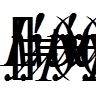при наявності лінійних крайових умов

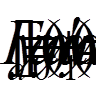
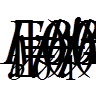(8)

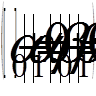
Оберемо кінцеву систему базисних функцій ( = 0, 1, . , n), що складають частину деякої повної системи, причому потурбуємося, щоб функція 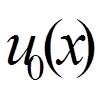задовольняла неоднорідні крайові умови

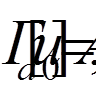
а функції 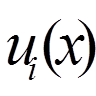( = 1, 2, . . . , n) задовольняли б однорідним крайовим умовам

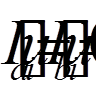( = 1, 2, . . . , n).

Розв’язок крайової задачі (7) – (8) будемо, як звичайно, шукати у вигляді

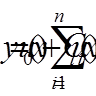(9)

При нашому підборі базисних функцій 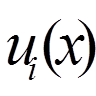функція 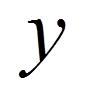, що визначається формулою (9), очевидно, задовольняє крайовим умовам (8) при будь-якому виборі коефіцієнтів 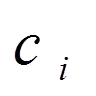. Вираз (9) підставимо у диференціальне рівняння (7), що дає нев’язність

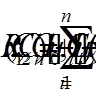
Для точного розв’язку у нашій крайовій задачі функція 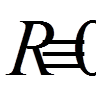; тому для отримання наближеного розв’язку, близького до точного, нам вигідно підібрати коефіцієнти 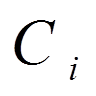так, щоб функція 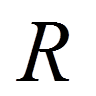була в якомусь сенсі малою.