Курсовая работа: Метод Галеркіна пошуку розв’язку лінійної крайової задачі
і враховуючи при цьому ортогональність системи тригонометричних функцій
(1,  ,
,  ,
,  ,
,  , . . .)
, . . .)
 ,
,  ,
,
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  .
.
Виконуючи відповідні скорочення, приходимо до системи

з якої одержуємо  ,
,  ,
,  . Таким чином маємо
. Таким чином маємо
 .
.
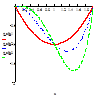
В таблиці 1 наведено для порівняння значення отриманого наближеногорозв’язку і точного розв’язку 
Наближений і точний розв’язок задачі (11), (12)
Таблиця 1:
 | - | 0 |  |
 | 1.429 | 2 | 3.714 |
 | 1.368 | 2 | 3.718 |
| Приклад розв'язання крайової задачі методом Галеркіна в середовищі Mathcad |
| Постановка задачі: |
| Серед усіх функцій y(x), визначених на інтервалі [a;b] і задовольняючих крайовим умовам y(a)=0 і y(b)=0 потрібно знайти таку, яка задовольняла б диференціальному рівнянню p(x)y''+q(x)y'+r(x)y+k(x)=0 |
| Вихідні дані: |
| Границі інтервала: |
 |
 |
| Функція p(x): |
 |
| Функція q(x) |
 |
| Функція r(x) |
 |
| Функція k(x): |
 |
| Розрахункові формули: |
| Алгебраїчні базисні функції: |
 |
 |
 |
| Число членів у сумі Рітца |
 |
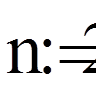 |
| Формування систем лінійних алгебраїчних рівнянь метода Галеркіна для випадку алгебраїчних базисних функцій: |
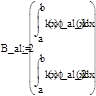
A_al_2:= [на дискеті, Галеркін.mcd]
| Число членів у сумі Рітца |
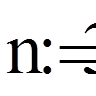 |

A_al_3:= [на дискеті, Галеркін.mcd]
| Розв'язання задачі |
| Розв'язання систем рівнянь - визначення коефіцієнтів сум Рітца: |
| Номер останнього утримуваного члена суми Рітца |
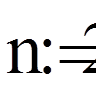 |
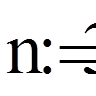 |
|
Алгебраїчні базисні функції: |
 |
 |
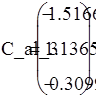 |
| Задання кроку табулювання сум Рітца: |
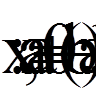 |
| Побудова розв'язків у вигляді сум Рітца: |
| Алгебраїчні базисні функції: |
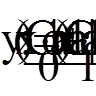 |
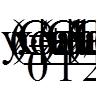 |
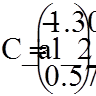 |
 |
 |

Результати отримані за допомогою створеної програми


ВИСНОВОК
Математичне моделювання процесів і явищ в різних галузях науки і техніки є одним з головних способів отримання нових знань і технологічних рішень. В наш час коли життя людини вже майже неможливе без електронно-обчислювальної техніки, всі процеси автоматизуються, а задачі, які потребували деякого часу і зусиль тепер виконуються за лічені хвилини.
Чисельні методи один із напрямів розробки пошуку оптимальних розв’язків математичних задач та пошуку саме того методу, який би давав найбільш точний результат. Моя робота присвячена одному з методів пошуку розв’язку лінійної крайової задачі – методу Галеркіна. Даний метод досить зручний для пошуку розв’язку у вигляді аналітичного виразу.
В першій частині курсового проекту розглянута постановка задачі, в якій наведено опис методу. В математичній моделі описано безпосередньо сам метод Галеркіна та його основні принципи.
Друга частина мого курсового проекту починається з опису алгоритму методу Галеркіна для пошуку розв’язку лінійної крайової задачі. В алгоритмі містяться головні кроки пошуку розв’язку лінійної крайової задачі за даним мені методом.За цим алгоритмом наведений тестовий приклад, а також написана програма в середовищі MicrosoftVisualC++, текст якої знаходиться в додатку А. До даного методу складена блок-схема алгоритму.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1.Капченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М: Наука, 1972. – 369 С.
2.Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Физматгиз, 1960. - 659с.
3.Калиткин Н.Н. Численные методы. - М.: Наука, 1978. - 512с.
4. Бахванов Н. С., Жидков Н.П. Кобельков Г.М. Чисельные методы електронный вариант учебника.
5. Белашов В. Ю., Чернова Н. М. Эффективные алгоритмы и программы вычислительной математики. Магадан: СВКНИИДВОРАН, 1997. 160 с.
6. Культін Н.Б. Программирование в Turbo Pascal 7.0 и Delphi. – СПб: BHV-Санкт-Петербург, 1999. – 234с.
ДОДАТОК А
ТЕКСТ ПРОГРАМИ МОВОЮ MicrosoftVisualC++
MainFrm.cpp
#include "StdAfx.h"
#include "example.h"
#include "MainFrm.h"
#ifdef _DEBUG