Курсовая работа: Метод Галеркіна пошуку розв’язку лінійної крайової задачі

Наскільки цей наближений розв’язок близький до точного, в загальному випадку питання залишається відкритим. Таким чином, для визначення коефіцієнтів 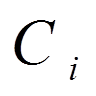( = 1, 2, . . . , n) приходимо до системи лінійних рівнянь

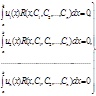
або, більш детально,

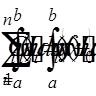(10)

( = 1, 2, . . . , n).

РОЗДІЛ 2. ПРАКТИЧНА ЧАСТИНА

2.1. Алгоритм методу

1.Визначаємо з даного диференціального рівняння другого порядку функції

.

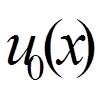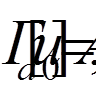
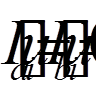2. Обираємо систему базисних функцій ( = 0, 1, . . . , n) так, щоб функція задовольняла крайовим умовам: а функції ( = 1, 2, . . . , n) задовольняли б однорідним крайовим умовам (= 1, 2, . . . , n).

3. Знаходимо 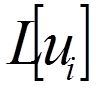( = 0, 1, 2, 3, 4).

4. Використовуючи позначення

,

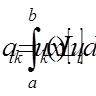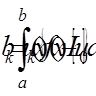
обраховуємо коефіцієнтисистеми:

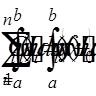( = 1, 2, . . . , n).

5. Виконуючи необхідні скорочення приходимо до системи з якої визначаємо 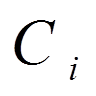( = 1, 2, . . . , n) і отримуємо розв’язок вигляді:

.

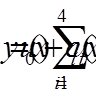2.2. БЛОК-СХЕМА АЛГОРИТМУ

Метод Галеркіна

ͳ

Так

ͳ

Так

Обрахунок ( = 0, 1, 2, 3, 4)

Обрахунок ,

2.3.Тестовий приклад

Методом Галеркіна знайти наближений розв’язок рівняння,

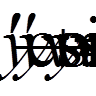, (11)

що задовольняє крайовим умовам

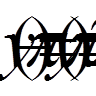. (12)

Розв’язання:

Оберемо в якості системи базисних функцій 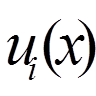(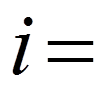0, 1, 2, 3, 4) наступні тригонометричні функції:

, , , , .

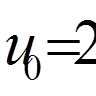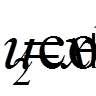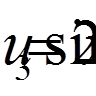Ці функції лінійно незалежні на відрізку , причому функція задовольняє крайовій умові (12), а інші функції – нульовим крайовим умовам. Будемо шукати розв’язок у вигляді

.

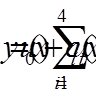Знаходимо 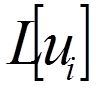( = 0, 1, 2, 3, 4):

,

,

,

,

,

.