Курсовая работа: Метод кусочного размножения оценок при обработке реализаций сигналов ограниченного объема

Выделение трех участков связано с тем, что в начале и конце реализации оценивание происходит по группам оценок различного объема. На первом интервале исходной выборки , количество оценок полезной составляющей в каждый момент времени пропорционально номеру отсчета , на втором интервале – количество оценок равно ширине скользящего интервала и составляет значение, а на последнем интервале оценивания , с ростом номера отсчета количество оценок в каждом сечении уменьшается от до 1 (рис. 1).

Оценка исходного ряда (5) представляет собой также матрицу такого же размера :

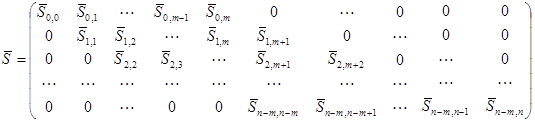. (6)

Матрица (6) получается в результате оценивания полезной составляющей по значениям , , каждой строчки матрицы (5). Для перехода от матричного представления оценки обратно к одномерной реализации необходимо усреднить ее значения по столбцам. Результирующая оценка полезной составляющей запишется в следующем виде:

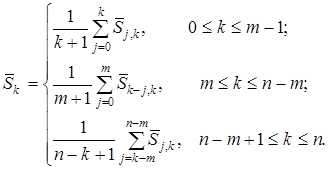(7)

Значения оценок, составляющие матрицу (6), получены путем аппроксимации исходной реализации , для каждого методом наименьших квадратов. Таким образом, соответствует номеру строки матрицы оценок (6). В работе [9] приведены результаты исследования для случая, когда на каждом интервале производится аппроксимация функциями пространства (2), при этом оно ограничено условием . Полученные результаты являются частными и не позволяют исследовать зависимость погрешности оценивания от параметров метода обработки. Для проведения таких исследований необходимо получить общее решение задачи аппроксимации на каждом скользящем участке для аппроксимирующего полинома произвольной степени . Использование ранее предложенного подхода имеет следующие недостатки [5]:

- минимизация целевой функции метода наименьших квадратов при произвольной степени аппроксимирующего полинома сводится к решению системы уравнения, что приводит к значительным вычислительным затратам при больших ;

- в случае, если необходимо увеличить или уменьшить степень аппроксимирующего полинома, производится полный пересчет всех ранее полученных коэффициентов и оценок.

Использование системы ортогональных многочленов позволяет устранить эти недостатки.

Исходная дискретная последовательность определена в узле. Введем систему ортогональных многочленов Лежандра, где последовательно возрастающих степеней, обладающие свойством [5]:

,

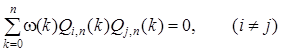где – некоторая весовая функция. Будем рассматривать случай, когда .

Таким образом, имея систему ортогональных многочленов, можно построить многочлен наилучшего приближения в смысле минимума квадратичной целевой функции. В общем случае аппроксимирующую полиномиальную функцию можно представить в виде [5]:

. (8)

Отметим, что полином (8) также принадлежит к пространству (2).

В соответствии с общей теорией ортогональных многочленов коэффициенты определяются выражением [5]:

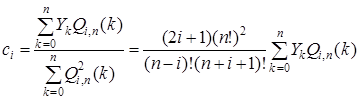, (9)

где 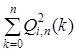– норма ортогональных многочленов.

В соответствии с предлагаемым методом разбиения оценки коэффициентов полинома (8) на каждом скользящем интервале различны, тогда выражение (9) перепишется в следующем виде:

,

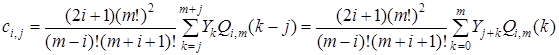где , – длина интервала разбиения.

Анализ выражения для показывает, что коэффициенты зависят не только от степени полинома, но и от номера интервала . В соответствии с выражением (7) результирующая оценка полезного сигнала через системы ортогональных многочленов запишется в следующем виде:

кусочное размножение оценка сигнал

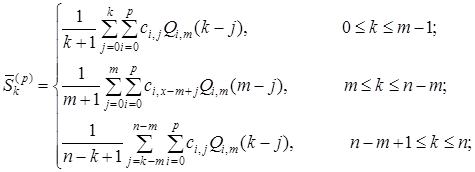(10)

где индекс в показывает степень аппроксимирующего полинома на каждом скользящем интервале.

Выражение (10) представляет собой обобщенное уравнение, которое позволяет получить оценку полезной составляющей предлагаемым способом разбиения с последующей аппроксимацией на каждом скользящем интервале полиномом произвольной степени . Так как пространство аппроксимирующих функций (2) ограничено условием , то на основе выражения (10) можно получить частные случаи при , и [9].

В случае, когда , выражение (10) запишется в следующем виде:

(11)

При выражение (10) имеет вид: