Курсовая работа: Метод Монте Карло и его применение

Глава 3. Вычисление интегралов методом Монте-Карло.

§1. Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода.

Пусть необходимо вычислить линейный функционал , где , причём для интегрального оператора K с ядром выполняется условие, обеспечивающее сходимость ряда Неймана: . Цепь Маркова определяется начальной плотностью и переходной плотностью ; вероятность обрыва цепи в точке равна . N – случайный номер последнего состояния. Далее определяется функционал от траектории цепи, математическое ожидание которого равно . Чаще всего используется так называемая оценка по столкновениям , где , . Если при , и при , то при некотором дополнительном условии . Важность достижения малой дисперсии в знакопостоянном случае показывает следующее утверждение: если и , где , то , а . Моделируя подходящую цепь Маркова на ЭВМ, получают статистическую оценку линейных функционалов от решения интегрального уравнения второго рода. Это даёт возможность и локальной оценки решения на основе представления: , где . Методом Монте-Карло оценка первого собственного значения интегрального оператора осуществляется интерациональным методом на основе соотношения . Все рассмотренные результаты почти автоматически распространяются на системы линейных алгебраических уравнений вида . Решение дифференциальных уравнений осуществляется методом Монте-Карло на базе соответствующих интегральных соотношений.

§2. Способ усреднения подынтегральной функции.

В качестве оценки определённого интеграла принимают

,

где n – число испытаний; - возможные значения случайной величины X, распределённой равномерно в интервале интегрирования , их разыгрывают по формуле , где - случайное число.

Дисперсия усредняемой функции равна

,

где 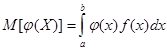, . Если точное значение дисперсии вычислить трудно или невозможно, то находят выборочную дисперсию (при n>30) , или исправленную дисперсию (при n<30) , где .

Эти формулы для вычисления дисперсии применяют и при других способах интегрирования, когда усредняемая функция не совпадает с подынтегральной функцией.

В качестве оценки интеграла , где область интегрирования D принадлежит единичному квадрату , , принимают

, (*)

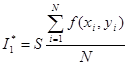где S – площадь области интегрирования; N – число случайных точек , принадлежащих области интегрирования.

Если вычислить площадь S трудно, то в качестве её оценки можно принять ; в этом случае формула (*) имеет вид

,

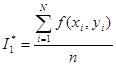где n – число испытаний.

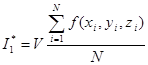В качестве оценки интеграла , где область интегрирования V принадлежит единичному кубу , , , принимают , где V – объём области интегрирования, N – число случайных точек , принадлежащих области интегрирования.

Если вычислить объём трудно, то в качестве его оценки можно принять , в этом случае формула (**) имеет вид 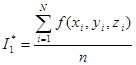, где n – число испытаний.

Задача: найти оценку определённого интеграла .

Решение. Используем формулу . По условию, a=1, b=3, . Примем для простоты число испытаний n=10.Тогда оценка 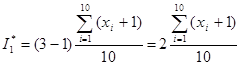, где возможные значения разыгрывается по формуле .