Курсовая работа: Метод Ньютона и его модификации решения систем нелинейных уравнений
Наличие оценки (1.8) позволяет сформулировать следующий практический критерий окончания итерации метода Ньютона. При заданной точности ![]() вычисления нужно вести до тех пор, пока не окажется выполнимым равенство:
вычисления нужно вести до тех пор, пока не окажется выполнимым равенство:
![]() . (1.9)
. (1.9)
Пример 1.
Используя метод Ньютона, найдём с точностью ![]() положительный корень уравнения
положительный корень уравнения ![]() .
.
![]() Для
Для ![]() имеем
имеем ![]() . Очевидно, что
. Очевидно, что ![]() , т.е.
, т.е. ![]() -простой корень. Возьмём начальное приближение
-простой корень. Возьмём начальное приближение ![]() и будем выполнять итерации метода Ньютона по формуле:
и будем выполнять итерации метода Ньютона по формуле:
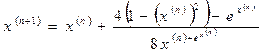 .
.
Результаты первых итераций с 10 знаками мантиссы приведены в табл. 1.
Табл. 1
При ![]() вычисления следует прекратить, и после округления получим
вычисления следует прекратить, и после округления получим ![]() .
.
Сравнение результатов итераций со значением ![]() показывает, что приближения
показывает, что приближения ![]() содержат 1, 3, 6 верных значащих цифр соответственно. Это подтверждает отмеченный ранее факт, что при каждой итерации метода Ньютона число верных значащих цифр примерно удваивается.
содержат 1, 3, 6 верных значащих цифр соответственно. Это подтверждает отмеченный ранее факт, что при каждой итерации метода Ньютона число верных значащих цифр примерно удваивается.
Пример 2.
Используя метод Ньютона, укажем итерационный процесс вычисления ![]() , где
, где ![]() ,
, ![]() - натуральное число.
- натуральное число.
По определению, ![]() - это неотрицательная величина, удовлетворяющая равенству
- это неотрицательная величина, удовлетворяющая равенству ![]() . Таким образом, задача сводится к вычислению положительного корня уравнения
. Таким образом, задача сводится к вычислению положительного корня уравнения ![]() , где
, где ![]() . Итерационная формула метода Ньютона имеет вид:
. Итерационная формула метода Ньютона имеет вид:
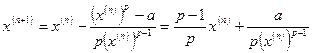 . (1.10)
. (1.10)
2. МЕТОД НЬЮТОНА И ЕГО РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
2.1. ОПИСАНИЕ МЕТОДА.
Обобщим метод Ньютона, изложенный в пункте 1 для решения одного нелинейного уравнения, на решение систем нелинейных уравнений. При этом будем исходить из трактовки метода Ньютона как метода линеаризации.
Предположим, что исходя из начального приближения ![]() к решению
к решению ![]() построены приближения
построены приближения ![]() . Заменим в системе
. Заменим в системе
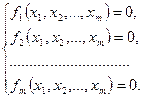 (*)
(*)
каждую из функций ![]() линейной частью её разложения по формуле Тейлора в точке
линейной частью её разложения по формуле Тейлора в точке ![]() :
:
![]() .
.
В результате придём к системе линейных алгебраических уравнений:
![]() ,
,
![]() ,
,
. . . . . . . . . . . . . . .
![]() ,
,
имеющей в матричной форме записи вид:
![]() . (2.1)
. (2.1)
Здесь ![]() - матрица Якоби.
- матрица Якоби. 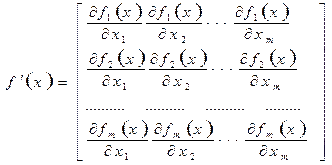 .
.
Предположим, что матрица ![]() невырожденная, т.е. существует обратная матрица
невырожденная, т.е. существует обратная матрица ![]() . Тогда система (2.1) имеет единственное решение, которое принимается за очередное приближение
. Тогда система (2.1) имеет единственное решение, которое принимается за очередное приближение ![]() к решению
к решению ![]() . Таким образом, приближение
. Таким образом, приближение ![]() удовлетворяет равенству:
удовлетворяет равенству:
![]() , (2.2)
, (2.2)
выражая из которого ![]() , выводим итерационную формулу метода Ньютона:
, выводим итерационную формулу метода Ньютона:
![]() . (2.3)
. (2.3)
Замечание.
Формула (2.3) предполагает использование трудоёмкой операции обращения матрицы, поэтому непосредственное её использование для вычисления ![]() в большинстве случаев нецелесообразно. Обычно вместо этого решают эквивалентную системе (2.2) систему линейных алгебраических уравнений:
в большинстве случаев нецелесообразно. Обычно вместо этого решают эквивалентную системе (2.2) систему линейных алгебраических уравнений:
![]() (2.4)
(2.4)
относительно поправки ![]() . Затем полагают:
. Затем полагают:
![]() (2.5)
(2.5)
2.2. СХОДИМОСТЬ МЕТОДА.
Сформулируем основную теорему о сходимости метода Ньютона.
Теорема 3.
Пусть в некоторой окрестности решения ![]() системы (*) функции
системы (*) функции ![]() дважды непрерывно дифференцируемы и матрица
дважды непрерывно дифференцируемы и матрица ![]() невырождена. Тогда найдётся такая малая
невырождена. Тогда найдётся такая малая ![]() - окрестность решения
- окрестность решения ![]() , что при произвольном выборе начального приближения
, что при произвольном выборе начального приближения ![]() из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка:
из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка:
![]() ,
, ![]() .
.
Эта оценка означает, что метод сходится с квадратичной скоростью.
Квадратичная скорость сходимости метода Ньютона позволяет использовать простой практический критерий окончания:
![]() . (2.6)
. (2.6)
Пример 3.
Используя метод Ньютона, найдём с точностью ![]() решение
решение ![]() ,
, ![]() системы
системы ![]() .
.