Курсовая работа: Метод Ньютона и его модификации решения систем нелинейных уравнений

Как и в одномерном случае методы секущих и Стеффенсена теряют устойчивость вблизи решения (фактически это происходит при попадании приближения в область неопределённости решения ). Поэтому при использовании этих методов важно вовремя прекратить выполнение итераций.

4. ЧИСЛЕННЫЙ ПРИМЕР

Начальное приближение:

Вектор-функция:

Матрица Якоби вектор-функции:

Вычисляем корень по формуле метода Ньютона c точностью :

k
0	0 -1	-0.841 0	-1.06 0.54 0 -2	-0.944 -0.255 0 -0.5	-0.794 -1	0.794>
1	-0.794 -1	0.295 0.63	-1.821 -0.221 -1.588 -2	-0.608 0.067 0.482 -0.553	-0.657 -0.794	0.247>
2	-0.657 -0.794	0.058 0.062	-1.48 0.12 -1.314 -1.588	-0.633 -0.048 0.524 -0.59	-0.617 -0.788	0.040>
3	-0.617 -0.788	-0.0000597 0.011	-1.441 0.159 -1.234 -1.588	-0.639 -0.064 0.497 -0.58	-0.616 -0.788	0.001=
4	-0.616 -0.788	0.000522 0.0004	-1.434 0.166 -1.232 -1.576	-0.639 -0.067 0.5 -0.582	-0.616 -0.788	0<

Ответ:

5. ЛИСТИНГ ПРОГРАММЫ НА ЯЗЫКЕ MATHCAD

Вводим вектор функцию:

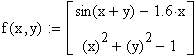
Функция iter(x,y) вычисляет следующее приближение к корню по формуле Ньютона , где

,

,

,

:

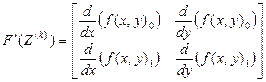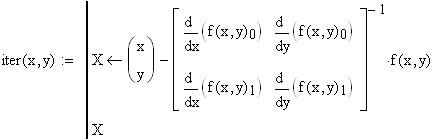
Функция norma(x,y,x1,y1) вычисляет норму между текущим и следующим приближением:

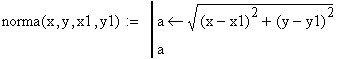
Функция Newton(x,y,eps) находит решение системы уравнений с точностью до eps:

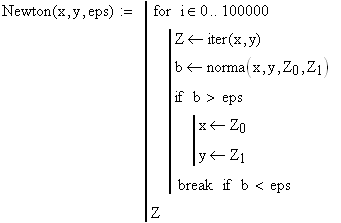
Найдем решение заданной системы нелинейных уравнений при начальном приближении x=0, y=-1, с точностью до 0.001:

Полученное решение совпадает с рассчитанным.

ЗАКЛЮЧЕНИЕ

В данной курсовой работе был представлен метод Ньютона. Если оценивать качество метода по числу необходимых итераций, то следовало бы отметить, что этот метод стоит применять всегда, когда он сходится. Трудность использования метода Ньютона не только сохраняются при применении его к решению систем нелинейных уравнений, но и усугубляются из-за возникающей проблемы вычисления на каждой итерации матрицы из частных производных, что само по себе может оказаться весьма сложным делом.

Существует большое число модификаций метода Ньютона, позволяющих в тех или иных ситуациях снизить его трудоёмкость либо избежать необходимости вычисления производных. Такие модификации были также рассмотрены в данной курсовой работе: упрощённый метод Ньютона, использования формул численного дифференцирования, метод ложного положения, метод секущих, метод Стеффенсена.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.