Курсовая работа: Метод Ньютона и его модификации решения систем нелинейных уравнений

Результаты вычислений с шестью знаками мантиссы приведены в табл. 2.

Табл. 2

При критерий окончания выполняется и можно положить , .

2.3. ТРУДНОСТИ ИСПОЛЬЗОВАНИЯ.

Трудности использования метода Ньютона не только сохраняются, но и усугубляются. Во-первых, возникает проблема вычисления на каждой итерации матрицы из частных производных, что само по себе может оказаться весьма сложным делом. Во-вторых, обостряется проблема нахождения хорошего начального приближения. Её решить в многомерном случае гораздо труднее, чем в одномерном.

3. МОДЕФИКАЦИЯ МЕТОДА НЬЮТОНА.

Если оценивать качество метода Ньютона только по числу необходимых итераций, то следовало бы сделать вывод о том, что этот метод стоит применять всегда, когда он сходится. На практике для достижения разумной точности при выборе достаточно хорошего начального приближения требуется, как правило, 3-5 итераций.

Однако при оценке общеё трудоёмкости метода следует учитывать, что на каждой итерации требуется выполнение следующей дополнительной работы:

1) вычисление компонент вектора ;

2) вычисление компонент матрицы Якоби ;

3) решение системы линейных алгебраических уравнений (2.4).

Существует большое число модификаций метода Ньютона, позволяющих в тех или иных ситуациях снизить его трудоёмкость либо избежать необходимости вычисления производных. Рассмотрим кратко некоторые из таких модификаций.

3.1. УПРОЩЁННЫЙ МЕТОД НЬЮТОНА.

Заменим в расчётных формулах метода Ньютона (2.4), (2.5) матрицу , зависящую от , постоянной матрицы . В результате получим расчётные формулы упрощённого метода Ньютона :

, (3.1)

. (3.2)

Этот метод сходится со скоростью геометрической прогрессии, если начальное приближение выбрано достаточно близким к решению , причём знаменатель прогрессии тем меньше, чем ближе к .

По сравнению с методом Ньютона число итераций, необходимое для достижения заданной точности , существенно возрастает. Тем не менее общие вычислительные затраты могут оказаться меньше. Причины этого состоят в следующем. Во-первых, вычисление матрицы Якоби производится здесь только один раз; во-вторых при использовании упрощённого метода Ньютона (3.1), (3.2) многократно решается система линейных уравнений с фиксированной матрицей и различными правыми частями. Это означает, что при решении систем (3.1) методом Гаусса возможно применение LU– разложения матрицы , которое резко уменьшает число операций, необходимых для вычисления .

3.2. ИСПОЛЬЗОВАНИЕ ФОРМУЛ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ.

Довольно часто вычисление производных , являющихся элементами матрицы , затруднено или вообще невозможно. В такой ситуации для приближения вычисления производных можно использовать формулы численного дифференцирования.

Например, можно использовать следующую конечно-разностную аппроксимацию производной:

.

Параметры - это конечно-разностные шаги .

Если в расчётных формулах метода Ньютона (2.4), (2.5) заменить матрицу аппроксимирующей её матрицей с элементами , то получим следующий итерационный метод:

, (3.3)

. (3.4)

В простейшем варианте этого метода шаги не зависят от . Отметим, что выбор величины шагов представляет собой не очень простую задачу. С одной стороны, они должны быть достаточно малыми, чтобы матрица хорошо приближала матрицу , с другой стороны, они не могут быть очень малы, та как в этом случае влияние погрешностей вычисления функций на погрешность формулы (3.3) численного дифференцирования становится катастрофическим (выполняется вычитание близких приближённых чисел).

Следующие три метода можно рассматривать как варианты метода (3.3), (3.4), в которых реализованы специальные подходы к вычислению вектора . Для того чтобы приведённые ниже рассуждения были формально корректными, в формуле (3.3) положим , если оказалось, что .

3.3. МЕТОД ЛОЖНОГО ПОЛОЖЕНИЯ.

Пусть - фиксированный вектор. Положим . Тогда формулы (3.3), (3.4) определяют метод ложного положении, обладающий линейной скоростью сходимости в случае, если вектор и начальное приближённое выбраны достаточно близко к решению.

3.4. МЕТОД СЕКУЩИХ.

Можно связать задание последовательности с какой-либо сходящейся к нулю векторной последовательностью, например, с последовательность невязок или поправок . Так, полагая , где j=1,…n , a k=1,2, …, приходим к простейшему методу секущих — обобщению скалярного метода секущих:

, (3.5)

где

,

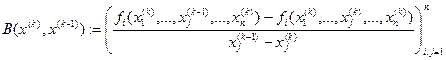k =1,2,3,… .

Этот метод является двухшаговым и требует задания двух начальных точек и . При п = 1 сходимость метода (3.5) имеет порядок . Можно рассчитывать на такую же скорость и в многомерном случае.

К методу секущих так же, как и к методу Ньютона, можно применить пошаговую аппроксимацию обратных матриц на основе метода Шульца. Расчетные формулы этой модификации легко выписать, заменив в совокупности формул ААМН (аппроксимаиионный аналог метода Ньютона) 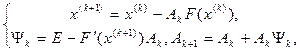матрицу на матрицу

из (3.5).

3.5. МЕТОД СТЕФФЕНСЕНА.

Вычисления по методу Стеффенсена производят по формулам (3.3), (3.4), где .

Замечательно то, что хотя этот метод не требует вычисления производных и в отличие от метода секущих является одношаговым, он, как и метод Ньютона, обладает свойством квадратичной сходимости. Правда, как и в методе Ньютона, его применение затруднено необходимостью выбора хорошего начального приближения.