Курсовая работа: Методы отсечения

(29)

и максимизирует значение функции

(30)

Будем предполагать, что проранжированы, т.е. и являются наперед заданными числами.

Теорема. Пусть x(£_k , C) – оптимальное решение задачи (27–28, 30), – элементы симплексной таблицы, соответствующей ему.

Если x(£_k , C) является недопустимым решением задачи (27–30) и , тогда, используя i-ю строку симплексной таблицы, можно построить отсечение, обладающее свойством правильности по формулам:

(31)

(32)

где

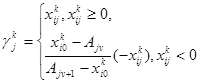(33)

Доказательство. Проверим вначале условие отсечения. Пусть в оптимальном решении x(£_k , C) координата не удовлетворяет условию (29). Покажем, что в этом случае вектор х(£_k , C) не удовлетворяет условиям (31, 32). Поскольку N_k – множество индексов небазисных переменных x_{i ,} которые в оптимальном решении равны нулю, то равенство (31) принимает вид и будет отрицательным согласно условию теоремы. Следовательно, , т.е. условие отсечения не выполняется.

Проверим условие правильности. Для этого покажем, что любое допустимое решение задачи (27–30) удовлетворяет условиям (31, 32).

Запишем разложение для координаты допустимого решения задачи (27–30) по небазисным переменным

(34)

и рассмотрим два случая: a) ; б) . Введем обозначения:

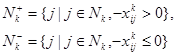
и представим (34) в виде

где

Очевидно, так как .

Рассмотрим случай а): , или что все равно, .

Отсюда Но поэтому

(35)

Домножим обе части (35) на неотрицательную величину и сложим с неотрицательной величиной :

(36)

Рассмотрим случай б): или, что все равно, Так как по определению , то Умножим обе части неравенства на неотрицательную величину и на -1, получим . Прибавляя к полученному выражению неравенство , получим

(37)