Курсовая работа: Методы отсечения
(38)
Формула (38) определяет правильные отсечения. Сравнивая ее с выражением (31–32), приходим к выводу, что коэффициенты 
определяются следующим образом:
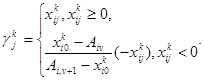
Теорема доказана.
Алгоритм Дальтона – Ллевелина может быть описан следующим образом.
1. Решается (£k , C) – задача (27–30) (вначале k = 0). Пусть x(£k , C), k = 0, 1, 2,… оптимальное решение (£k , C) – задачи, 
– симплексная таблица.
2. Проверяется условие допустимости по всем координатам оптимального вектора решения х(£k , C) (£k , C) – задачи. Если условие допустимости выполняется, то полученное решение является оптимальным решением исходной задачи (27–30). Если условие допустимости не выполняется хотя бы по одной координате, осуществляется переход к 3.
3. Пусть 
не удовлетворяет условию допустимости. Тогда выбирается
i 0 = min { i | 1< i < n 1 , х j 0 k – не удовлетворяет (29)}.
4. Для выбранного номера i = i 0 строится правильное отсечение, т.е. вводится дополнительная переменная
где 
определяется формулой (33),
5. Добавляем линейное ограничение, определяющее правильное отсечение, к условиям (£k , C) – задачи и получаем новую (£k +1 , C) – задачу. Полагая k = k + 1 , переходим к п. 1.
Приведем без доказательства теорему о конечности алгоритма.
Теорема. Если: коэффициенты целевой функции дискретны; F ( x ) ограничена снизу на многогранном множестве £; задача (£, C) имеет по крайней мере одно решение; выбор строки для построения правильного отсечения производится по правилу минимального номера и (£k , C) – задачи решаются методом последовательного уточнения оценок, то алгоритм Дальтона и Ллевелина сходится.
6. Алгоритм Данцига
Способ построения правильных отсекающих плоскостей, предложенный Данцигом значительно проще, чем все изложенные выше способы. Но, как показали Гомори и Гофман, конечность алгоритма Данцига гарантируется лишь для очень узкого класса задач. На примере алгоритма Данцига видно, насколько тонким является вопрос о построении правильных отсечений и сколь осторожно следует подходить к различным упрощенным алгоритмам.
Рассматривается полностью целочисленная задача линейного программирования:
Максимизировать
(39)
при условиях
(40)
(41)
– целые, 
(42)
Ранг матрицы 
считаем равным m.
Теорема . Пусть x(£r , C)=xr является оптимальным опорным планом задачи (£r , C) и xr не удовлетворяет условию целочисленности, Nr – множество индексов, нумерующих небазисные переменные, соответствующие xr .
Тогда неравенство