Курсовая работа: Методы решения задач линейного программирования с n-переменными
Необходимо определить нормы выпуска каждого вида продукции, чтобы прибыль от её реализации была максимальной.
Построение экономико-математической модели
Прибыль обозначим F, тогда F=c1 x1 +c2 x2 +...+cn xn g max
Составим ограничения для первого ресурса:
а11 - объем первого ресурса, который расходуется на производство одной единицы первого вида продукции;
а11 x1 - объём первого ресурса, который требуется на изготовление x1 единиц первого вида продукции;
а12 x2 - объём первого ресурса, который требуется на изготовление x2 единиц второго вида продукции;
а1n xn - объём первого ресурса, который требуется на изготовление xn единиц n-ого вида продукции;
а11 x1 +a12 x2 +...+a1n xn - объём первого ресурса, который требуется на изготовление продукции, следовательно, мы имеем следующее ограничение:
а11 x1 +а12 +...+а1n xn <=b1
Аналогично для остальных ресурсов:
а21 x1+а22 +...+а2n xn <=b2
а31 x1+а32 +...+а3n xn <=b3
...
аm1 x1 +аm2 +...+amn xn <=bm
Кроме того, количество выпущенной продукции не может быть отрицательной, следовательно, x1 >= 0, x2 >=0, ...,xn >=0.
Таким образом, получаем следующую экономико-математическую модель задачи линейного программирования:
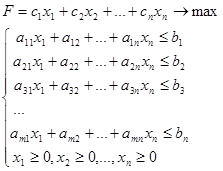 (2.1)
(2.1)
Задачу линейного программирования для N (любое целое число) переменных можно представить в следующем виде:

Решения, удовлетворяющие системе ограничений условий задачи и требованиям неотрицательности, называются допустимыми, а решения, удовлетворяющие одновременно и требованиям минимизации (максимализации) целевой функции, — оптимальными .
С помощью графического метода может быть решена задача линейного программирования, система ограничений которой содержит n неизвестных и m линейно независимых уравнений, если N и M связаны соотношением N – M = 2.
Действительно, пусть поставлена задача линейного программирования.
Найти максимальное значение линейной функции
Z = c1 х1 +c2 х2 +... +cN xN
при ограничениях
a11 x1 + a22 x2 + ... + a1N ХN = b1
a21 x1 + a22 x2 + ... + a2N ХN = b2
. . . . . . . . . . . . . . .