Курсовая работа: Методы решения задач линейного программирования с n-переменными
III. 55255,72+4,35x2 +7,188x4 =0
-4,35x2 -7,188x4 =55255,72
x2 = -12702,464-1,652x4
| x2 | -11050,464 | -3817,536 |
| x4 | -1000 | -10000 |
Построим область допустимых решений задачи, ограниченную прямыми:
x2 =1063,172-0,17x4 (I)
x4 =646,229-0,371x2 (II)
x2 = -12702,464-1,652x4 (III)
Найдем max:
![]()
![]()
![]()
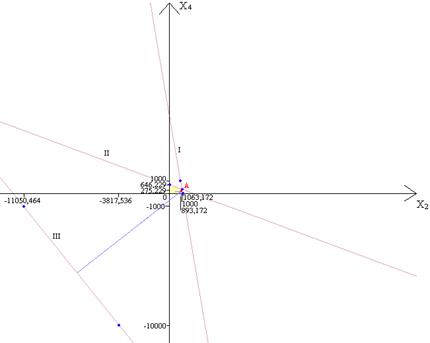
Рис. 1 График функции
Построим линию уровня 55255,72+4,35x2 +7,188x4 =0 и вектор градиента (4,35; 7,188). Будем передвигать линию уровня, пока не выйдем из многоугольника, что произойдет в точке A с координатами (1061; 257). В этой точке функция принимает максимальное значение 63330.
Ответ: Чтобы достичь максимальной прибыли предприятие должно выпустить 1061 изделий товара B и 257 изделий товара D.
Решение задачи симплекс-методом
Решим прямую задачу линейного программирования симплекс-методом. Определим максимальное значение целевой функции F(X) = 30x1 +50x2 +62x3 +40x4 при следующих условиях:
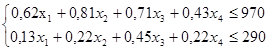
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
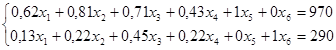
![]()
Выразим базисные переменные x5 и x6 через небазисные.
![]()
![]()
Переходим к основному алгоритму симплекс-метода.
Поскольку задача решается на максимум, то переменную для включения в текущий план выбирают по максимальному положительному числу в уравнении для x0 .
![]()
![]()
В качестве новой переменной выбираем x3 .
Вычислим значения D3 по всем уравнениям для этой переменной